Mortality Differentials by Lifetime Earnings Decile: Implications for Evaluations of Proposed Social Security Law Changes
Social Security Bulletin, Vol. 73, No. 1, 2013 (released February 2013)
To evaluate the distributional effects of some proposed Social Security law changes, such as an increase in Social Security's early entitlement age, retirement policy analysts typically tabulate the number of workers who fall below a predetermined threshold of hardship. Analysts using this technique often implicitly assume that the insured population falls neatly into a low-earnings poor health group and a remaining good health group. If the hardship threshold assumption is correct, there should be no difference in mortality risk between lifetime earnings deciles above a hardship threshold. This study finds that the hardship threshold model is overwhelmingly rejected in US Social Security data, a result consistent with similar studies conducted in Canada, Germany, and England. The bottom 80–95 percent of the male lifetime earnings distribution exhibits an inverse correlation with regard to mortality risk (the higher the earnings, the lower the mortality risk) at ages 63–71.
Hilary Waldron is an economist with the Division of Economic Research, Office of Research, Evaluation, and Statistics, Office of Retirement and Disability Policy, Social Security Administration.
Acknowledgments: The author thanks Harriet Duleep, Howard Iams, Javier Meseguer, and David Pattison for their helpful comments and suggestions.
Contents of this publication are not copyrighted; any items may be reprinted, but citation of the Social Security Bulletin as the source is requested. The findings and conclusions presented in the Bulletin are those of the authors and do not necessarily represent the views of the Social Security Administration.
Introduction
| AIME | average indexed monthly earnings |
| AWI | average wage index |
| CWHS | Continuous Work History Sample |
| EEA | early entitlement age |
| FRA | full retirement age |
| MBR | Master Beneficiary Record |
| MEF | Master Earnings File |
| OASDI | Old-Age, Survivors, and Disability Insurance |
| OECD | Organisation for Economic Co-operation and Development |
| PIA | primary insurance amount |
| SSA | Social Security Administration |
| tax max | taxable maximum |
The distributional effects of some proposed Social Security law changes (for example, an increase in Social Security's early entitlement age (EEA)) are at least partially dependent on the distribution of health and mortality risk throughout the fully insured Social Security–covered worker population. To evaluate these types of proposals, retirement policy analysts typically tabulate the percentage of survey respondents who self-report poor (or fair) health or a work-limiting health condition and/or who score below a threshold of hardship, where the hardship level is specified by the analyst rather than estimated. By using a threshold model to evaluate these policy proposals, retirement analysts implicitly assume that only workers who fall below the threshold will be adversely affected by the proposed law change. However, in order for these analyses to accurately describe the distributional effects of proposed Social Security law changes, fully insured workers must be equal in their health, mortality risk, and "ability to work" above the threshold chosen by the analyst.
To test the hardship threshold assumption most commonly used by retirement analysts, this analysis estimates mortality differentials at ages 63–71 by lifetime earnings decile. If the hardship threshold assumption is correct, there should be no difference in mortality risk between lifetime earnings deciles above a poverty or hardship threshold. The study finds that the hardship threshold model is overwhelmingly rejected in data from the Social Security program in the United States, a result consistent with similar studies conducted in Canada, Germany, and England.
I find that the male population does not appear to be homogenous above a low poverty or hardship threshold. Instead, the point above which the male population of Social Security fully insured retired workers becomes statistically indistinguishable with respect to mortality risk at ages 63–71 ranges from the top 5 to top 20 percent of the lifetime earnings distribution. At least the bottom 80 percent of the male lifetime earnings distribution exhibits an inverse correlation with regard to mortality risk (the higher the earnings, the lower the mortality risk).
Under current law, the link between earnings and benefit levels and the equal application of age-of-entitlement rules, regardless of earnings levels, means that a worker is never penalized for additional work or thrift. Because the insured population does not fall neatly into a low-earnings poor health group and a remaining good health group, attempts to target a subset of badly disadvantaged workers by altering the benefit rules that apply equally to everyone could both miss the intended target and introduce work disincentives into a program currently designed to reward work. Analysts using a threshold model to predict the success of legislative attempts to target less-than-healthy workers may misestimate the targeting effects by a potentially large, unknown, and unmeasured margin.
Background
Mortality differentials by socioeconomic status have been documented since at least the seventeenth century (Antonovsky 1967). Throughout history, researchers have found that death rates are higher among individuals of lower socioeconomic status. The relationship between higher death rates and lower socioeconomic status might be a gradient in which mortality rates continue to decline as socioeconomic status increases, or it might take the form of a threshold in which the higher death rates are concentrated below some threshold, and above that threshold there are no differences in mortality by socioeconomic status. Studies that assume that adverse mortality is limited to individuals below a threshold often assume that the threshold is defined as being in a state of poverty or being in some other state of hardship. That assumption will therefore be referred to in this article as a poverty threshold or hardship threshold model. The alternative assumption that mortality declines more gradually with socioeconomic status, without a clear threshold above which the graded relationship between mortality and socioeconomic status disappears, will be referred to as the gradient model.
Among researchers using a poverty threshold model, the definition of "poverty" tends to vary; few restrict themselves to the Census Bureau definition of poverty that is used by many means-tested programs in the United States. Whatever the definition, those researchers assume that a line or threshold exists between individuals who are in adverse circumstances, with worse health and higher mortality, and those who are not, with better health and lower mortality. Although threshold models often assume a graded relationship below the threshold, with extremely adverse circumstances leading to higher mortality and reductions in mortality up to the threshold, the assumption is that over the threshold any further increases in status do not lead to additional improvements in death rates or health (Adler and Stewart 2010, 7). Another way of describing the assumption of the threshold model is that above the threshold, health and mortality are homogeneous, or equal, with regard to socioeconomic status, but below the threshold, health and mortality may be heterogeneous and is certainly worse than above the threshold.
Marmot (2004, 4) describes the threshold assumption as the idea that the "health gap is confined to poor health for the disadvantaged, 'them,' and good health for everybody else, 'us.'" He describes the alternative gradient model as implying that "wherever we are in the social hierarchy, our health is likely to be better than those below us and worse than those above us."
The threshold model can be assumed, rather than tested, or a threshold can be arbitrarily specified and tested by measuring mortality or health above and below that threshold. The data tend to support threshold models, tested in this way, against the alternative that there are no differences in mortality and health between individuals above and below the threshold. Before the mid-1980s, as described by Adler and Stewart (2010, 7), a majority of research tended to follow this approach.
It is possible, however, to allow the empirical data to determine the shape of the relationship between socioeconomic status and mortality or health and to test the threshold assumption against the gradient assumption. Provided a researcher has enough detail in the underlying data, the threshold assumption can be tested with standard statistical techniques and then only used in a model if the population he or she is seeking to analyze truly demonstrates the threshold. As the data available to researchers have improved1 and as a multitude of researchers have tested and rejected the threshold assumption against the observable data, the epidemiological and public health literature have moved strongly toward widespread acceptance of the idea that a gradient model best describes the pattern of health and mortality differentials observed in most wealthy, developed Organisation for Economic Co-operation and Development (OECD) countries, including the United States.
Although there were studies before the 1980s examining the possibility of a gradient (such as Kitagawa and Hauser (1973)), Adler and Stewart (2010) described the movement to gradient models in the public health field as occurring with the publication of results from the Whitehall study by Marmot, Shipley, and Rose (1984), which found a positive monotonic correlation between occupational grade and health and mortality. (The higher the occupational grade, the better the health and the lower the mortality). In part, the Whitehall study wielded such influence on the field because the data allowed the authors to cleanly test the gradient hypothesis. (The original Whitehall population consisted of men employed by the British civil service. All were above the poverty line and had access to health care.2)
The retirement literature (in the United States), on the other hand, still tends to assume a poverty or hardship threshold model.3 There are several possible reasons for this disconnect between public health researchers and retirement researchers. First, the public health literature is predominately concerned with differentials below age 65, while the retirement literature is concerned with differentials above age 65. The data available to adequately estimate mortality differentials at older ages are limited, and the data that do exist are generally not publicly available to a wide range of users because of data confidentiality and disclosure concerns. Second, because mortality differentials tend to narrow with age, there may be a tendency on the part of some researchers to assume mortality differentials are not important at older ages. Finally, the retirement literature often lacks an interdisciplinary focus and tends to suffer from a paucity of citations to noneconomic (that is—public health, epidemiological, or medical) journals. For these reasons, the poverty or hardship threshold model has been perpetuated in the retirement literature to the extent that at least one strand of the current retirement literature (in the United States) now lags current epidemiological literature by about 25 to 30 years in its analytical orientation.
Differences in analytical orientation often spill over into differences in interpretation of health trends. For example, while public health researchers have tended to focus on differences in health disaggregated by socioeconomic status and are generally concerned with a trend toward increased disparities (Adler and Stewart 2010, 1; National Center for Health Statistics 1998, 2012; Department of Health and Human Services 1999), retirement researchers have tended to focus on aggregate trends, and many are optimistic about those trends (Steuerle 2011; Burtless 1998; Shoven 2007).
The focus of this article is on the effects of differences in mortality risk by lifetime earnings deciles on proposals to change the EEA for Social Security retired-worker benefits in the United States. The dominant model used to evaluate the distributional effects of changes to the EEA is analytically very close to the poverty threshold model. Many analysts assume (without measuring) that the population of workers eligible for retirement benefits falls into two groups: (1) a group below some hardship threshold whose members cannot extend their working lives because of poor health and (2) a remaining group above the hardship threshold with no differentials in health or mortality. EEA proposals are evaluated under this assumption by counting the number of workers under the assumed threshold who have claimed benefits early, or more broadly, the number of fully insured workers who fall below the threshold criteria at a certain age or ages.
A central problem with this method of analysis is that the statistical technique does not allow the analyst to observe a gradient in workers' health and mortality risk above the predetermined threshold, even if one actually exists in the underlying data. Additionally, there does not appear to be any clear way to estimate the uncertainty around a policy estimate based on a hardship threshold model because there is no clear and obvious way to calculate an error band around an analyst's judgment of what constitutes hardship or ability to work.
Some analysts define adverse circumstance as having an adverse health condition; others combine adverse health conditions with adverse financial conditions. Just as the definition of poverty can vary by analyst, so too can the definition of "adverse" or "poor" health. Adverse health is sometimes interpreted to mean a health condition that limits one's ability to work. The definition of the term ability to work can also vary by researcher as can the definition of a related concept—what set of job characteristics constitutes a "physically demanding job." The fact that empirical estimates can vary based on how poverty or hardship is defined (Kingson and Arsenault 2000; Smith 1999) creates an additional uncertainty for policymakers attempting to formulate proposals based on this method of research.
This study seeks to use a relatively simple and objective measure of health (mortality) and a more standardized measure of financial condition (position in the lifetime earnings distribution) to test the hypothesis that poor health and mortality among older men follow a threshold model.4 By asking a policy question in terms of measurable mortality risk (either you are dead or you are not) rather than an amorphous, subjective ability to work or hardship criteria, we can apply more rigorous statistical techniques to the data and more accurately assess the effects (and the uncertainty surrounding those effects) of a proposed policy change on the underlying population of fully insured workers.
In this way, an examination of whether mortality risk follows a poverty threshold model at older ages can also be used as a test of whether common techniques used to evaluate changes to Social Security's first age of eligibility for retired-worker benefits (currently age 62)5 are based on accurate assumptions regarding the distribution of health and mortality risk in the exposed (that is, fully insured) population. In other words, if the assumption of homogeneity above the threshold is rejected, then the actual distributional effects of a policy change could differ from the change predicted when using a threshold model by a potentially large, unknown and unmeasured margin.
After discussing previous literature estimating mortality gradients at older ages, I discuss the data and methodology used in this study, followed by estimates of male mortality risk by male lifetime earnings deciles. I then examine the implications of those results for the view that an increase in the EEA will increase the general revenue of the Treasury. Next, to further explore proposals that seek to target workers below a hardship threshold for protection from proposed increases in the EEA, I estimate female mortality risk by male lifetime earnings deciles and compare female death rates with male death rates at equivalent earnings deciles. Finally, to explore alternative ways of focusing on fairly long-lived individuals, I measure the distribution of workers at the Social Security—Old-Age, Survivors, and Disability Insurance (OASDI)—taxable maximum (tax max) by earnings decile and sex. I conclude with a brief discussion on the difficulty of targeting subgroups effectively through the retired-worker benefit, given the universality of the benefit's design.
Previous Literature
While the literature on mortality differentials is extremely large, the number of studies providing estimates of mortality gradients at older ages is smaller, and research providing estimates of mortality gradients throughout the entire income distribution at older ages is even smaller still. Unlike the United Kingdom, the United States (and many other OECD countries) has not traditionally collected socioeconomic data on death certificates.
Consequently, studies in wealthy, developed OECD countries testing mortality gradients along the entire earnings distribution at older ages using lifetime or "permanent" earnings measures have often relied on administrative data from national pension plans. Such pension plan data combine career earnings data from an individual's working years with mortality data from an individual's retirement years.
One strength of this type of analysis is that there is typically a gap between the career earnings measure and the ages over which death is observed, which eliminates the problem of a sudden health shock to earnings that would both place an individual in a low socioeconomic category (even if he or she had been a high earner prior to the shock) and increase the risk of death. In addition, even without a large gap between the last year of earnings and the observation of the year of death, mathematically, a sudden 1-year shock to a high earner would not have so great an impact on a career average earnings measure that he or she would drop into the low-lifetime-earner category. Because a lifetime earnings measure will capture the influence of chronic poor health on hours worked and employment, such a measure may also have predictive power through the ability to capture causal effects running from both poor health to earnings and earnings to health.6
In the United States, Duleep (1986) was one of the first researchers to exploit Social Security administrative earnings and death data to estimate mortality differentials by income, although her focus was mainly below age 65.7 At the time of her 1989 work, Duleep suggested using Social Security data to measure mortality rates over time using "constant income percentiles rather than constant income categories" (349). Taking up that suggestion, Waldron (2007) used the Social Security Administration's (SSA's) Continuous Work History Sample (CWHS)—capped Social Security earnings data that were then imputed by Waldron—and found male mortality differentials at older ages widening between the top and bottom half of the lifetime earnings distribution over the 1972–2001 period. Using a mix of capped and uncapped Social Security earnings data matched to the Survey of Income and Program Participation (SIPP), Cristia (2007) found some evidence of a mortality gradient by lifetime earnings quintile at ages 50–64 (the standard errors are large enough for the confidence intervals to cross, but the parameter estimates indicate a gradient), although, in an unusual result, found less evidence of a gradient between the bottom three deciles than between the top two quintiles at ages 65–75.
As described in the methodology section, this study further builds on the percentile technique suggested in Duleep (1989), by exploiting the availability of longitudinal earnings data over the OASDI tax max beginning in 1982. By using that data, one can test for mortality differences throughout the entire earnings distribution, free of any possible biasing effects caused by the capping of data at the OASDI tax max. Because the taxable maximum has changed over time, analyses that use capped (or imputed) earnings data will have problems estimating mortality differences accurately at the upper end of the career earnings distribution.
Studies most closely related to this analysis include those by Wolfson and others (1993) on the national Canadian pension plan data and Shkolnikov and others (2008) on the national German pension plan data. The measure of socioeconomic status used was earnings from ages 45 through 64 in the case of Wolfson and others (1993) and a measure roughly corresponding to earnings over an entire working lifetime in the case of Shkolnikov and others (2008).
In describing the shape of the relationship between mortality risk and earnings, with deaths observed from ages 65 through 70, Wolfson and others (1993, S175) noted that their results were "not consistent with a 'threshold' relationship where poverty is associated with poorer health and longevity, but that above some low income level, income and health are independent." Instead, they found that men in the 10th–82nd percentiles of the earnings distribution experience lower longevity at ages 65–70 than the top 18 percent of the earnings distribution. The authors also found that the gap between the other percentiles and the top was larger at the lower percentiles than the higher percentiles.8
Shkolnikov and others (2008) divided the male earnings distribution into quintiles and observed that a mortality gradient persisted from the 20th through 80th percentile of the earnings distribution beginning at age 65 and remained significant at ages 80 plus.9 While the age standardized mortality ratio at ages 65 plus was 1.6 for quintile 2 versus quintile 5, the difference between quintile 4 and quintile 5 was still a statistically significant 1.24.
The persistence of mortality gradients high up the earnings distribution in the Canadian and German pension data matches British data from the Whitehall study—an analysis of a sample of British civil servants—in which the British civil service employment grade at ages 40–69 was found to predict mortality risk 25 years later (van Rossum and others 2000). In addition, although 81 percent of a Whitehall follow-up sample had been in the middle grades in contrast to 7 percent in high employment grades at ages 40–69, Breeze and others (2001) found that workers in the middle employment grades had a statistically significant risk of poor health and poor physical performance, roughly 30 years later, when compared with the high grades. As Marmot and Brunner (2005) wrote, "although early life determinants, life-course factors, and current circumstances all have effects on disease risk in older age, the preeminent determinants observed in the [Whitehall II] cohort are adult socioeconomic position and work-based determinants from mid-life."
Methodology
The data set used in this analysis was created by merging several internal SSA research files, all of which contain individuals selected based on Social Security's CWHS selection criteria. The 1 percent CWHS sample "may be described as a stratified cluster probability sample of all possible SSN's [Social Security numbers] " (Smith 1989). To create the data set, a 2008 active10 CWHS extract was merged to a 2010 Master Beneficiary Record (MBR) extract, a 2009 Numident extract, and a 2009 Master Earnings File (MEF) extract. An individual had to appear on both the active CWHS extract and Numident extract and be born from 1937 through 1945 to be included in the data set (N = 272,234). For this study, the CWHS provides annual OASDI taxable earnings data and quarters of coverage information from 1951 through 2008. The MEF provides annual earnings reported to the Internal Revenue Service, including earnings in employment not covered by Social Security and earnings in Social Security–covered employment that exceed the OASDI tax max from 1982 through 2008.11 The MBR is used to identify Social Security disabled-worker beneficiaries and as a source of demographic data. The MBR contains records of individuals who have filed Social Security (OASDI) claims. The Numident is used as a source of demographic data and is the primary source of death data for individuals who do not have an MBR record.
Unlike some research in the public health field, this study is more narrowly focused on differential mortality as it relates to Social Security policy. For that reason, I make several restrictions to the sample, that, while relevant to proposals to change the law with regard to Social Security's retired-worker benefit, have the effect of biasing the sample toward healthier and longer-lived individuals. First, disabled-worker beneficiaries are deleted from the sample (N = 42,114) because, in theory, individuals who have been determined to be disabled under current-law definitions would not be affected by many legislative proposals that apply to the retired-worker population, such as proposals that increase Social Security's EEA.12 Next, insured status at age 61 is calculated for the remaining individuals in birth cohorts 1937–1945, and only those fully insured for retired-worker benefits are included (N = 179,886). Those individuals were newly eligible for retired-worker benefits at age 62 in the 1999–2007 period. To be fully insured for retired-worker benefits, workers born in 1929 or later must have had 40 quarters of coverage or 10 years of work. From a public health perspective, the elimination of individuals who were not fully insured and Social Security disabled-worker beneficiaries would tend to eliminate those at the highest risk of death because of strong links between labor force attachment and health (particularly for men). Finally, individuals had to have lived until at least age 63 to be included in the final data set, so that all workers would have had an equal opportunity to claim Social Security retired-worker benefits at the age-62, current-law EEA (N = 164,777).13 Of the total number of workers in the sample universe, 85,863 were men and 78,914 were women. My main analysis only examines mortality estimates for men because a woman's own earnings may be a poor proxy for her socioeconomic status or household income, given low rates of labor force participation for at least some part of the lifetime of the female birth cohorts under study. In a later section of this article, I conduct a sensitivity analysis that measures death rates for women by both male and female lifetime earnings deciles. Although my measure of female socioeconomic status is poor, the sensitivity analysis is conducted because some policy options seek to apply correlations between Social Security's average indexed monthly earnings (AIME) amount, income, health, and life expectancy for men toward all low-earning, retired-worker beneficiaries.
In order to classify workers into lifetime earnings groups, this analysis uses a definition of lifetime earnings expected to be highly correlated (for men) with the measure of lifetime earnings that Social Security uses to calculate retired-worker benefits. Under current law, Social Security's primary insurance amount (PIA) is the amount from which all Social Security benefits payable on a worker's earnings record are based.14 As explained on Social Security's website,15 to compute a PIA for a fully insured worker eligible for a retired-worker benefit, SSA takes the highest of up to 35 years of earnings of an individual,16 indexes those earnings to general wage levels (as measured by the average wage index (AWI17)), sums those indexed earnings, and divides the total amount by up to 35 years, resulting in an AIME amount. The PIA is calculated as the sum of three separate percentages of portions of the AIME.18 These percentages of the PIA formula are fixed by law at 90 percent, 32 percent, and 15 percent (referred to here as PIA factors), while the dollar amounts (or bend points) in the formula are indexed to the AWI and differ annually with changes in the AWI.
Because Social Security's AIME is a lifetime measure, interpretation of the AIME is complicated by large changes in the level of the OASDI tax max over time. The OASDI tax max was close to the average wage in the 1950s and 1960s and was not continuously indexed to the national AWI until 1982. In this article, the birth cohorts I analyze (aged 18 in the 1955–1963 period) experienced large growth in the taxable maximum relative to the national AWI over their lifetimes. Although capping of the earnings amounts at the taxable maximum will not affect a median, as long as the median is below the capped level, the capping of earnings will affect deciles above the median if the cap (that is, taxable maximum) is below the uncapped level of earnings for that decile. Accordingly, this study uses an alternative lifetime earnings measure that takes advantage of uncapped earnings data available in Social Security's MEF. While, under current law, Social Security's AIME is calculated based on OASDI taxable earnings, which are taxed only up to the OASDI tax max ($106,800 in 2011), Social Security's MEF contains earnings data on all earnings reported to the Internal Revenue Service, including earnings in Social Security–covered employment over the OASDI tax max and earnings in employment not covered under Social Security from 1982 to the present time.19 Because earnings over the OASDI tax max are only observable beginning in 1982, a top 35-year measure more comparable to the AIME but including earnings above the taxable maximum cannot be calculated using Social Security administrative data for birth cohorts fully insured for retired-worker benefits at age 61 without substantial imputation of earnings capped at the taxable maximum. Imputation techniques, by their nature, add more uncertainty to the data and are unlikely to achieve the precision needed to divide the earnings distribution into deciles, particularly at the upper end of the earnings distribution and in years when the OASDI tax max was low relative to the average wage. Results could also be sensitive to the choice of imputation technique.
In order to create earnings deciles roughly based on all earnings in the US economy, ages 45–55 are chosen as a proxy for lifetime earnings because those ages occur at the peak of the earnings distribution.20 Peak earnings are a strong proxy for lifetime earnings because earnings at the peak will capture fulfilled earnings potential.21 Earnings from ages 45 through 55 for each individual are measured relative to the national AWI that corresponds to the year the earnings are recorded in the administrative earnings records. The earnings are then averaged over ages 45–55. To avoid unintended interactions between year of birth and earnings level, the percentile of the earnings distribution in which an individual falls is based on the distribution of average earnings for that individual's year of birth. Because average relative peak earnings are used to place workers into deciles, the decile placement using the peak measure would most likely differ from an uncensored top-35 placement (could one be calculated) if an individual had high earnings at younger ages and low earnings in middle ages. Because an individual's wage reflects returns to experience, such a scenario is not representative of the typical age-earner profile, which tends to be hump shaped. Thus, in general, a peak lifetime earnings measure would be expected to be strongly correlated with a top-35 lifetime earnings measure, with workers with high relative peak earnings also having high relative AIMEs.
However, because of changes in Social Security coverage over time, certain groups—such as some state and local workers, and federal employees and some employees of nonprofit organizations hired prior to 1984—will have low AIMEs from Social Security–covered wages (that is, from jobs held when young) and high peak earnings not covered by Social Security (that is, from their primary job). In addition, foreign-born workers who emigrate from their native countries to the United States at older ages may have low AIMEs and high peak earnings because of a large number of zeroes in their earnings records at younger ages. To address these problems, this analysis shows results both with or without those groups (see the Appendix for the all inclusive and restricted samples).
In terms of mortality risk, groups not covered by Social Security—for example, federal employees hired prior to 1984 and some state and local workers—will be well captured by my age 45–55 measure because that measure will include their primary wages not covered by Social Security. The foreign born, on the other hand, may be selectively healthier than the native born, regardless of lifetime earnings decile. Such an effect would be observed if individuals who immigrate to the United States tend to have better health than others—that is, if it is more difficult to immigrate in poor health than good health. It is also not clear that the earnings patterns of the foreign born are analytically equivalent to the native born (Duleep and Dowhan 2008) so that a male immigrant falling in the same earnings decile as a native-born man could be different from his native-born counterpart on many dimensions.
The main lifetime earnings measure used in this study includes years of zero earnings from ages 45 through 55. I have no information on the reason for a zero year of earnings in Social Security administrative data. A zero representing voluntary early retirement or a yearlong voluntary vacation, for example, would not necessarily be analytically equivalent to a zero representing a health shock, involuntary early retirement, or an unemployment spell. The former zero could be the result of an income (that is, wealth) effect and could potentially be either uncorrelated or negatively correlated with mortality risk, while the latter zero is more likely to be positively correlated with mortality risk. Therefore, the restricted sample is further limited through the use of a lifetime earnings average that excludes zeroes from ages 45 through 55 out of concern that some of the zeroes in the main measure could represent voluntary early retirement. A lifetime earnings average that includes zeroes that represent voluntary early retirement could potentially place some individuals in a lifetime earnings decile unrepresentative of (that is, lower than) their actual socioeconomic status.
While my all inclusive sample (Chart 1) is intended to depict the exposed population of fully insured workers, my restricted sample (Appendix, Chart A-1) is intended to bound the estimates, or test the sensitivity of the estimates to alternative definitions.
For the regressions results reported in this article, men are divided into deciles based on their position in the average relative earnings distribution from ages 45 through 55. Decile 1 is equal to the 0–10th percentile of the earnings distribution, decile 2 is equal to the 11th–20th percentile, and so on, so that decile 10 is equal to the 91st–100th percentile of the earnings distribution. Deciles 1 through 9 are modeled as dummy variables, with decile 10 modeled as the reference variable. To test the statistical significance of a possible mortality gradient by decile, each decile dummy variable is also tested against all other dummy variables. In other words, I measure the mortality risk of men in decile 1 against the risk of men in decile 2, decile 3, and so on. Then I measure the mortality risk of men in decile 2 against men in decile 3, decile 4, and so on. In this way, I can test the mortality threshold assumption. For example, if the sample is homogeneous with respect to mortality risk above the bottom 20 percent of the male lifetime earnings distribution, then the risk of death for men in decile 2 should be significantly higher than the risk of death for men in decile 3 by roughly the same magnitude as the risk of death for men in decile 2 relative to men in decile 10. Similarly, the risk of death for men in decile 3 should be equivalent to the risk of death for men at deciles 4, 5, 6, 7, 8, 9, and 10. In the middle of the distribution, the risk of death for men in decile 6 should be equivalent to the risk of death for men in deciles 3, 4, 5, 7, 8, 9, and 10. At the upper end of the distribution, the risk of death for men in decile 8 should be equivalent to the risk of death in decile 3, 4, 5, 6, 7, 9, and 10. In other words, we should see no evidence of a gradient, above, in this arbitrary example, decile 2. Empirically, the decile above which we cease to observe a gradient will serve as the estimated threshold decile. In this way, I use the observable data to determine a threshold as the point above which the data become homogeneous. In contrast, in much of the existing literature, the analyst makes a subjective assessment of what constitutes hardship and then measures what percentage of the exposed population falls below his or her predetermined level.
The model used to estimate mortality risk in this analysis is a discrete-time logistic regression, which is a type of survival model. Because survival time is measured in years for this study, the data include a large number of ties (that is, two or more events appearing to happen at the same time).22 The discrete-time logistic regression model is equivalent to the discrete-time proportional odds model proposed by Cox when there are many ties in the data (Allison 1995, 212). The model employs the simplifying assumption that events (deaths) occur at discrete times.23 The discrete-time logistic regression model allows for the incorporation of time-dependent variables, which for this analysis means that both age and year of birth can be included in the same regression, with age being measured as a time-dependent variable observed from the point of initial measurement until death or censoring.
Previous research that divided male Social Security–covered workers into the top and bottom half of the lifetime earnings distribution found that mortality differentials both narrowed by age and widened by birth cohort from ages 60 through 89 over birth cohorts 1912–1938 (Waldron 2007). The current study encompasses a narrower range of ages (63–71) and a narrower range of birth cohorts (1937–1945). Nevertheless, in theory, age and year-of-birth interactions may be present in the data. Unfortunately, it is difficult to model interactions and mortality differentials by decile at the same time because interactions tend to increase multicollinearity between variables, which will increase standard errors. This problem is compounded by the fact that, with the sample divided into 10 groups, a relatively small number of deaths within each decile can lead to larger standard errors than would be observed if lifetime earnings categories were divided into only 2 groups, for example. Finally, given that I employ nine ages and 9 years of birth, there will be multicollinearity between the age and year-of-birth variables, which may obscure a precise estimate on either variable. To solve that problem, I estimate two regressions: one that predicts the risk of death at ages 63–66 (observed for birth cohorts 1937–1945) and another that predicts the risk of death at ages 67–71 (observed for birth cohorts 1937–1941). As shown in the Appendix (Table A-1), standard errors are larger at ages 67–71 than at ages 63–66. Because the sample is smaller at ages 67–71, one cannot conclude that this result reflects greater uncertainty at the older ages; greater standard errors may instead be a reflection of a smaller sample size. Dividing the sample by age before regressing can therefore be seen as a more conservative test of the gradient hypothesis, in the sense that the smaller sample sizes of the two samples (that is, less deaths per sample) make it more difficult to find a gradient, should one exist. In other words, with a reduced sample size, it will be more difficult to reject the null hypothesis that men at all earnings deciles are at equal risk of death.
To produce estimates of mortality differentials, observations begin in the year the individual turns age 63 (or 67) and end in whichever comes first—the year of death or the end of the observation period (2008). The dependent variable is equal to 1 in the year the worker dies and 0 in every year the worker survives. Counting all annual observations for the 85,863 (43,637) individuals in the sample at ages 63–66 (or at ages 67–71), there are 2,936 (1,934) person-years in which a worker died and 274,088 (118,269) person-years in which a worker survived, for a total of 277,024 (120,203) pooled observations at ages 63–66 (67–71), respectively. The model measures the logit or log-odds of dying on these pooled observations using the maximum likelihood method of estimation.
As an additional test of my regression specifications, I conducted several further sensitivity tests of potential age and year-of-birth interactions (results not shown). First, I tested the statistical significance of interactions of earnings decile dummies with age and with year of birth for both the age 63–66 and age 67–71 regressions. Neither interaction was significant for either age group. Because the age 63–66 regression includes more birth cohorts than the age 67–71 regression, I further separated the age 63–66 sample in the following two ways: (1) ages 63–66, years of birth 1937–1941 and (2) ages 63–66, years of birth 1942–1945. Although this regression pushes the ability to model both age and year of birth to the outer limit, the same general pattern with respect to a mortality gradient by decile was found in the parameter results, albeit with some loss in significance on some individual parameter estimates that are due to the increase in standard errors created by the smaller subsamples.
Results
Similar to the findings of Wolfson and others (1993) who used Canadian data, Shkolnikov and others (2008) who used German data, and van Rossum and others (2000) who used British data, the poverty threshold hypothesis is strongly rejected in US data. Like Wolfson and others (1993) before me, I simply find no evidence that, above a low level of earnings or a poverty threshold, the lifetime earnings of men are uncorrelated with mortality at older ages. Instead, results strongly support the abundance of evidence from the public health field (Adler and Stewart 2010) that health and socioeconomic status are positively correlated (the higher the lifetime earnings, the better the health) throughout the entire lifetime earnings distribution.
Empirically, the lifetime earnings decile above which we observe no difference in mortality risk among men is the 10th decile (or top 10 percent of the earnings distribution24) at ages 63–66 (Appendix, Table A-1) and the top 5 percent of the earnings distribution at ages 67–71 (Appendix, Table A-2).25 Although the shape of the gradient is somewhat different at ages 63–66 than at 67–71, at all ages we see a clear inverse correlation between earnings decile and mortality risk (the higher the earnings decile, the lower the death rate). This is displayed in Chart 1, where I graph the death rates by decile that are predicted by the regressions results for ages 63–71 (see the Appendix, Table A-1). At ages 63–66, we see a sharp decline in the death rate from decile 1 to decile 2, a plateau from decile 2 to 3, a gradual decline from deciles 4 through 7, a plateau from deciles 7 through 8, and a gradual decline from decile 8 through decile 10. At ages 67–71, the decline in the death rate from decile 1 to decile 2 is less stark, but the decline from decile 3 to 4 is steeper. Deciles 4 through 7 exhibit a plateau, after which death rates again decline fairly steeply from deciles 7 through 10.
Death rates for fully insured males born in 1940, by age and male lifetime earnings decile
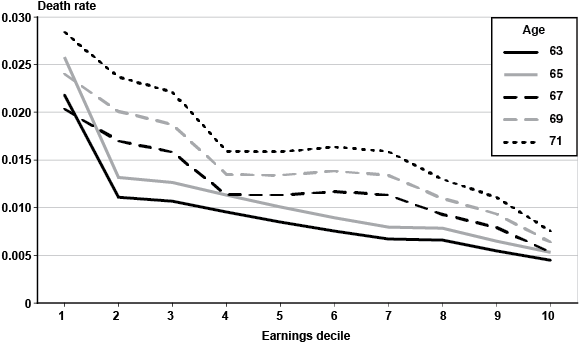
| Decile | Age 63 | Age 65 | Age 67 | Age 69 | Age 71 |
|---|---|---|---|---|---|
| 1 | 0.022 | 0.026 | 0.020 | 0.024 | 0.028 |
| 2 | 0.011 | 0.013 | 0.017 | 0.020 | 0.024 |
| 3 | 0.011 | 0.013 | 0.016 | 0.019 | 0.022 |
| 4 | 0.010 | 0.011 | 0.011 | 0.014 | 0.016 |
| 5 | 0.009 | 0.010 | 0.011 | 0.013 | 0.016 |
| 6 | 0.008 | 0.009 | 0.012 | 0.014 | 0.016 |
| 7 | 0.007 | 0.008 | 0.011 | 0.013 | 0.016 |
| 8 | 0.007 | 0.008 | 0.009 | 0.011 | 0.013 |
| 9 | 0.006 | 0.007 | 0.008 | 0.009 | 0.011 |
| 10 | 0.005 | 0.005 | 0.005 | 0.006 | 0.008 |
Tests of statistical significance of the mortality gradients observed visually in Chart 1 are displayed in Table 1. In this table, the odds ratios measure the odds of dying for men in the variable (left most) column of earnings deciles relative to men in reference deciles 2, 3, 4, 5, 6, 7, 8, 9, and 10. For example, men in decile 1 are 1.98 times (98 percent) more likely to die than men in decile 2 and 4.91 times (391 percent) more likely to die than men in decile 10 at ages 63–66. Results provide strong evidence of a mortality gradient in that a man's risk of death is generally predicted to be closer to a man in an adjacent decile than to a man in the top decile. For some adjacent deciles, such as deciles 2 and 3, the difference in the risk of death between men in one decile and the adjacent decile is statistically indistinguishable at ages 63–71. In such a case, if policymakers were to try to implement a policy option that protected decile 2 and below, for example, men in decile 3 could be better off attempting to qualify for the protected option because they are likely to be in no better health and have no greater longevity prospects than their counterparts in decile 2. In this way, policies based on thresholds when the exposed population exhibits a gradient could be subject to unintended behavioral responses.
| Variable | Decile 2 | Decile 3 | Decile 4 | Decile 5 | Decile 6 | Decile 7 | Decile 8 | Decile 9 | Decile 10 |
|---|---|---|---|---|---|---|---|---|---|
| Fully insured men aged 63–66 | |||||||||
| Decile 1 | 1.98* | 2.06* | 2.31* | 2.60* | 2.92* | 3.29* | 3.34* | 4.04* | 4.91* |
| (1.74–2.25) | (1.81–2.35) | (2.02–2.65) | (2.25–2.99) | (2.52–3.38) | (2.82–3.84) | (2.86–3.90) | (3.42–4.77) | (4.10–5.87) | |
| Decile 2 | 1.04 | 1.17*** | 1.31** | 1.47* | 1.66* | 1.68* | 2.04* | 2.48* | |
| (0.90–1.21) | (1.00–1.36) | (1.12–1.54) | (1.25–1.74) | (1.40–1.97) | (1.42–2.00) | (1.70–2.44) | (2.04–3.01) | ||
| Decile 3 | 1.12 | 1.26** | 1.41* | 1.60* | 1.62* | 1.96* | 2.38* | ||
| (0.96–1.31) | (1.07–1.48) | (1.20–1.67) | (1.34–1.9) | (1.36–1.92) | (1.63–2.35) | (1.96–2.89) | |||
| Decile 4 | 1.12 | 1.26** | 1.43* | 1.45* | 1.75* | 2.12* | |||
| (0.95–1.33) | (1.07–1.50) | (1.20–1.70) | (1.21–1.72) | (1.45–2.10) | (1.74–2.59) | ||||
| Decile 5 | 1.12 | 1.27** | 1.29** | 1.55* | 1.89* | ||||
| (0.94–1.34) | (1.06–1.52) | (1.07–1.54) | (1.28–1.88) | (1.54–2.31) | |||||
| Decile 6 | 1.13 | 1.14 | 1.38* | 1.68* | |||||
| (0.94–1.36) | (0.95–1.38) | (1.14–1.68) | (1.37–2.07) | ||||||
| Decile 7 | 1.01 | 1.23** | 1.49** | ||||||
| (0.84–1.23) | (1.00–1.50) | (1.21–1.84) | |||||||
| Decile 8 | 1.21*** | 1.47** | |||||||
| (0.99–1.48) | (1.19–1.82) | ||||||||
| Decile 9 | 1.22*** | ||||||||
| (0.98–1.52) | |||||||||
| Fully insured men aged 67–71 | |||||||||
| Decile 1 | 1.20** | 1.29* | 1.80* | 1.81* | 1.75* | 1.81* | 2.21* | 2.60* | 3.82* |
| (1.02–1.42) | (1.09–1.53) | (1.50–2.17) | (1.50–2.18) | (1.46–2.10) | (1.50–2.18) | (1.82–2.70) | (2.10–3.19) | (3.02–4.84) | |
| Decile 2 | 1.07 | 1.50* | 1.51* | 1.46* | 1.50* | 1.84* | 2.16* | 3.18* | |
| (0.90–1.28) | (1.24–1.81) | (1.25–1.82) | (1.21–1.76) | (1.25–1.82) | (1.51–2.25) | (1.75–2.67) | (2.50–4.05) | ||
| Decile 3 | 1.40* | 1.40* | 1.36* | 1.40* | 1.72* | 2.01* | 2.96* | ||
| (1.15–1.69) | (1.16–1.70) | (1.12–1.64) | (1.16–1.70) | (1.40–2.10) | (1.63–2.49) | (2.33–3.78) | |||
| Decile 4 | 1.00 | 0.97 | 1.00 | 1.23*** | 1.44** | 2.12* | |||
| (0.82–1.24) | (0.79–1.19) | (0.82–1.23) | (0.99–1.53) | (1.15–1.81) | (1.65–2.73) | ||||
| Decile 5 | 0.97 | 1.00 | 1.22*** | 1.43* | 2.11* | ||||
| (0.79–1.19) | (0.81–1.23) | (0.98–1.52) | (1.14–1.80) | (1.64–2.72) | |||||
| Decile 6 | 1.03 | 1.27** | 1.48* | 2.19* | |||||
| (0.84–1.27) | (1.02–1.57) | (1.19–1.86) | (1.70–2.81) | ||||||
| Decile 7 | 1.22*** | 1.44* | 2.11* | ||||||
| (0.99–1.52) | (1.15–1.80) | (1.64–2.72) | |||||||
| Decile 8 | 1.17 | 1.73* | |||||||
| (0.93–1.48) | (1.33–2.24) | ||||||||
| Decile 9 | 1.47** | ||||||||
| (1.13–1.93) | |||||||||
| SOURCES: Author's calculations based on Social Security administrative data files (1 percent 2008 active CWHS, 1 percent 2009 MEF, 1 percent 2010 MBR, and 1 percent 2009 Numident). | |||||||||
| NOTES: Sample consists of men born from 1937 through 1945 who were fully insured for retired-worker benefits; disabled-worker beneficiaries are excluded.
* = significant at the 1 percent level; ** = significant at the 5 percent level; *** = significant at the 10 percent level.
|
|||||||||
In addition, if policy analysts do not look for differences above a predetermined threshold when assessing specific proposals, policymakers using their analyses will be unaware of the distributional effects of policy options above the threshold. For example, in Table 1, men in deciles 3 and 4 at ages 63–66 are predicted to have a risk of death 2.38 and 2.12 times the risk of death of men in decile 10, respectively. In the middle of the distribution, men in deciles 5 and 6 are predicted to have a risk of death 1.89 and 1.68 times that of men in decile 10, while at upper end of the distribution, men in decile 9 are predicted to have a risk of death 1.22 times that of men in decile 10. This result stands in stark contrast to a threshold assumption that anyone above the bottom 20 percent of the lifetime earnings distribution (in our hypothetical example) will be equally affected by a policy change. In other words, the overwhelming rejection of the threshold hypothesis in SSA empirical data (Table 1) implies that because the Social Security retired-worker benefit rules are currently applied universally to all fully insured workers, analysts evaluating policy changes relative to current law need to include distributional effects on workers at all levels of the earnings distribution. Given the presence of a mortality gradient in SSA data, a threshold model is perhaps best reserved for evaluations of changes to a means-tested program, such as the Supplemental Security Income (SSI) aged program because workers above the SSI threshold would be ineligible for benefits and thus unaffected by any program changes.
The confidence intervals (the numbers in parentheses) in Table 1 provide additional information about the uncertainty of the estimates. Continuing with our hypothetical example in which a policy option is designed to protect the bottom 20 percent of male earners, we see that, at ages 63–66, even though the risk of death for decile 2 is significantly higher than the risk of death for men in decile 4, the point estimate for decile 4 (1.17) is within the confidence interval on the estimate of the odds of death for men in decile 2 versus decile 3 (0.9–1.21). This means that there is a statistical chance that men in decile 4 are equal in health and longevity risk to men in decile 3. In other words, because men in deciles 2 and 3 are indistinguishable, there is a chance that a proposal designed to apply to the bottom 20 percent of the male lifetime earnings distribution could be off by 20 percentage points and actually apply to the bottom 40 percent.
Overall, the most accurate advice that can be given to policymakers is that a policy change related to health and mortality differences among fully insured male workers will affect the top lifetime earnings decile the least, with adverse effects increasing as one moves down the earnings distribution, with the bottom decile being the most severely affected by the change. In other words, we have more certainty about the general pattern of the relationship between lifetime earnings and mortality risk than about the precision of any single point estimate (as is evident from the confidence intervals). Thus, one strength of the type of analysis used in this study is that the uncertainty of the predictions is explicitly measured. In contrast, in the type of analysis frequently employed by analysts using a threshold model that incorporates health variables, the uncertainty of the predictions is unmeasured.
As discussed in the methodology section, for completeness I also perform an identical analysis for a restricted analytical sample. The restricted sample eliminates the foreign born and workers with mostly non-OASDI taxable earnings for at least 5 years at ages 45–55. The sample is further restricted through the use of a lifetime earnings average that excludes zeroes at ages 45–55, out of concern that some of the zeroes could represent early retirement. As indicated in the Appendix (Chart A-1, Tables A-3 and A-4), the general pattern of the mortality gradients by lifetime earnings decile changes little with the change in sample. Most noteworthy is that at ages 63–66, decile 9 does not display a significantly higher risk of death than decile 10. Because the significance of decile 9 is close to being marginal in the all inclusive sample (see note 24), this result highlights the fact that our most conservative interpretation of results would place the point or threshold above which the population is homogeneous at no lower than the 80th percentile of the lifetime earnings distribution for the male fully insured population at ages 63–66.
Some analysts have proposed linking or indexing increases in either the EEA or full retirement age (FRA) to improvements in average life expectancy (Advisory Council on Social Security 1997 (options II and III); National Commission on Retirement Policy 1999; Aaron and Reischauer 2001; National Commission on Fiscal Responsibility and Reform 2010; Committee for a Responsible Federal Budget 2010). When evaluating those indexed proposals, distributional analysis based on a threshold model may give policymakers an inaccurate picture of the spread in life expectancy around the average. In contrast, using a gradient model may allow policymakers to more accurately assess the distributional effects of such an index at a point in time.
For example, Waldron (2007) found that if differences in rates of mortality improvement between the top and bottom half of the male lifetime earnings distribution observed over the 1972–2001 period continue, men born in 1941 in the top half of the earnings distribution would be expected to live 5.8 years longer than men in the bottom half of the distribution, up from a difference of 1.2 years observed for men born in 1912. The birth cohorts observed in this analysis (1937–1945) are not yet old enough for us to observe deaths at ages greater than 71. Therefore, there is not yet enough information available to replicate the trends analysis of Waldron (2007) with more detailed earnings categories. However, the results of this analysis do seem consistent with previous research that found that mortality risk has been greater for the bottom half of the male earnings distribution relative to the top half for at least 29 successive American birth cohorts whose members were born from 1912 through 1941.
Implications of the Gradient Model for Hypothesized Increases in General Revenue to the Treasury in Response to an Increase in the EEA
Many proponents of raising the EEA have argued that an increase in the EEA will increase the amount of tax money going to the general federal Treasury—that is, the amount of money available to be spent on the non-Social Security portion of the federal budget (Burkhauser 1996; Steuerle 2011; Aaron and Reischauer 2001; Biggs 2010; Johnson 2011). In the words of Johnson (2011), "It [an increase in the EEA] encourages people to work longer and earn more, easing pressure on both government and family budgets. Tax revenues increase when earnings rise, reducing the deficit and boosting funding for government programs." Aaron and Reischauer (2001) stated, "It [an increase in the EEA] would also enlarge the labor force, boost national production, and reduce the burden of supporting the economically inactive." The Committee for a Responsible Federal Budget (2010, 4) is even more enthusiastic, stating, "However, the earliest eligibility age is probably the most powerful lever we have to encourage longer working lives, which is critically important to increase economic growth."
The implicit assumption involved in this line of reasoning is that there will be an increase in general tax revenue coming to the Treasury from workers who would have stopped working at the current-law EEA of age 62 but who are induced to continue working until reaching the new, higher EEA, thereby continuing to pay federal income tax at, in theory, a higher rate than they would have paid if they had retired at age 62. Both the amount of new general revenue that analysts estimate will be raised through an increase in the EEA and the distributional incidence of what percentiles of the earnings distribution will contribute that new source of revenue to the federal Treasury depend on whether the population above the hardship threshold follows a gradient. In other words, under an assumption of homogeneity, all workers above the threshold will be equally affected by an increase in the EEA, relative to their current homogeneous behavior, and the incidence of the new source of revenue will be proportionately equal across the distribution of workers above the threshold.
However, in contrast to the underlying threshold assumption upon which hopes for new money appear to be based, several pieces of empirical evidence suggest that those hopes for new revenues could be overstated. In fact, existing empirical evidence suggests that the new revenues could be contributed roughly in reverse proportion to a worker's position in the earnings distribution (the higher the earnings decile, the less new money contributed). In other words, if higher earners are already the least likely to claim benefits at age 62 and the most likely to have private pension wealth with which they can offset an increase in the EEA, then any new monies not already being paid to the Treasury are likely to disproportionately come from lower earners who would prefer to retire at age 62, but who are liquidity constrained and cannot afford to retire without access to their retired-worker benefits. Although the terms "higher" and "lower" earners is used for ease of exposition, a key point is that existing empirical evidence suggests that any new revenues collected would follow a gradient (the higher the earnings, the less new revenue contributed), rather than a scenario in which those unable to work at all contribute no new money, and those able to work contribute new money in equal proportion to their position in the lifetime earnings distribution.
First, as shown in this study, the lifetime earnings of men are positively correlated with life expectancy, so that the higher the earnings the more incentive workers will have to remain in the workforce longer because of their longer expected lives, regardless of the EEA. Empirically, we also have evidence that higher earners and more educated workers already tend to disproportionately claim benefits at ages above the current-law EEA of 62 relative to lower-earning and lower-educated workers (Waldron 2001, 2004). In fact, Waldron (2004) found that workers in the high-earnings group claiming benefits at age 62 who were equal in health and mortality risk to those claiming later had private pension income in the top half of the earnings distribution. (Most men claiming benefits at age 62 in the high earnings group had health and mortality risk worse than those claiming later, regardless of the lifetime earnings of those claiming later; however, men with high private pension income were an exception to this general rule.) Given that the Social Security bend point formula only has a replacement rate of 15 percent at the top bend point (which hits at about the median of the male lifetime earnings distribution (Waldron 2012)), for high earners, a private pension may be likely to weigh more heavily in the retirement decision than the availability of a retired-worker benefit. Such workers may also be employed in jobs with generous early pensions because of a taste and preference for early retirement. If policy analysts wish to influence labor force participation behavior for this group, the tax treatment of the private pension would seem to be the more relevant policy lever. Of course, the long-run ability of policymakers to influence behavior would be limited by the extent to which workers could offset the policymakers' goals (that is, by simply moving money to an unconstrained vehicle).
In addition, a simple tabulation of the Current Population Survey by education level, sex, and year shows that at age 62 the labor force participation of men (and somewhat less strongly of women) is positively correlated with education level—the higher the education level, the more likely the respondent is in the labor force (Table 2). For example, the percentage of men in the labor force at age 62 in the 2009–2011 period was about 88 percent for those with a professional or doctorate degree, 67 percent for those with a bachelor's degree, 53 percent for high school graduates, and 46 percent for men without a diploma.26 The percentage of men who self-reported not being in the labor force at age 62 during the same period because of a disability was 27 percent for men without a diploma, 15 percent for high school graduates, 4 percent for those with a bachelor's degree, and 0 percent for those with a professional or doctorate degree (Table 2).
| Education level | Respondents in labor force | Respondents not in labor force because of a disability | ||
|---|---|---|---|---|
| Men | Women | Men | Women | |
| No high school diploma | 46 | 32 | 27 | 24 |
| High school graduate | 53 | 45 | 15 | 13 |
| Some college, no degree | 57 | 51 | 12 | 9 |
| Associate's degree | 62 | 55 | 12 | 12 |
| Bachelor's degree | 67 | 61 | 4 | 4 |
| Master's degree | 73 | 60 | 1 | 1 |
| Professional degree or doctorate | 88 | 77 | 0 | 6 |
| SOURCE: Author's tabulations based on selected years of the Census Bureau's March Supplement to the Current Population Survey. | ||||
Thus, we see evidence indicative of a gradient in labor force participation and self-reported disability; if all workers were homogeneous above a hardship threshold on those two dimensions, we would not expect to see differences in labor force participation rates and disability rates between doctors, lawyers, and men with doctorates compared with college and high school graduates. Women exhibit a similar pattern, although the percentage of them in the labor force is generally below that of men at identical educational categories, and we see less of a difference between women at higher levels of education. Partly, results for women at higher education levels may be caused by smaller samples of women at the higher education categories for the birth cohorts measured.
Additionally, Pattison and Waldron (2008, Chart 7) found that among men with positive earnings, the percentage who had elective deferrals (earnings funneled into a 401(k)-type pension plan arrangement) increased almost monotonically by earnings decile. (In other words, the higher the earnings decile, the greater the percentage of men who had elective deferrals.) In general, few men below the 4th decile had any elective deferrals. The percentage of men with elective deferrals rose less steeply over the 1990–2001 observation period for men in the 4th–6th deciles than for men in the 7th–10th deciles (ibid., 9). Trends were similar for women. Note that the elective deferral pattern followed a gradient; if elective deferral behavior was homogeneous above the hardship threshold, the percentage of workers above the threshold who had elective deferrals would not vary by earnings decile.
Overall, from the existing empirical evidence, we can infer that the bulk of any additional revenues from an increase in the EEA would come from workers who cannot afford to offset the retirement-age change through increased contributions to private pensions and personal savings accounts and who are not already working past age 62, but are able to work past that age. Because the federal income tax brackets are designed to be progressive, workers unable to offset the EEA increase would be disproportionately at lower tax brackets than one might assume if one were to believe that an increase in the EEA would apply universally across the earnings distribution (that is, in a poverty threshold world). Thus, new revenues would be less than they would be if all current age-62 retirees were alike with regard to labor force participation, disability, claiming, and personal saving behavior. The new revenues, furthermore, could be both regressive with regard to a primary worker's position in the earnings distribution and less than anticipated under a poverty threshold assumption. Of course, the evidence presented here is not thorough enough to be conclusive on these points. However, there is certainly enough empirical data going in the opposite direction from the implicit poverty threshold assumption underlying the belief that raising the EEA would increase the general revenue of the Treasury by a "substantial" amount for policymakers to consider asking proponents to provide a more detailed analysis of tax incidence by earnings decile.
Differences by Sex in Mortality Risk by Lifetime Earnings: Implications for Proposals to Target Benefit Changes on Workers Below a Hardship Threshold
Some policy analysts have recommended that the EEA be raised, but that the increase be accompanied by some type of "targeted" benefit to help those workers below the hardship (as defined by the analyst) threshold (Johnson 2011; Steuerle 2011; Munnell 2008; Burtless 1998). Targeted benefits include the following:
- Designing retired-worker program benefits specifically for the lower-earning and/or lower-income worker (Munnell 2008; Steuerle 2011).
- Targeted liberalization of the Disability Insurance (DI) program for workers below the new EEA (Burtless 1998; Johnson 2011).
- Extending unemployment benefits at ages 55 or older (Johnson 2011).
- Devoting more resources to retraining older workers (Johnson 2011).
- Expanding the SSI aged program (Burkhauser 1996; Johnson 2011; Biggs 2010).
Aaron and Reischauer (2001) suggest nontargeted liberalization of the DI program for workers between the old EEA and the new EEA.
One example of a proposal targeting workers in hardship by earnings level that is fairly straightforward to evaluate is that of Zhivan and others (2008). They propose setting the EEA based on AIME level, with the lowest AIME level having an EEA of 62 and the highest AIME level having an EEA of 64. The authors note, "an elastic EEA could potentially raise the earliest claiming age for most workers while shielding those for whom a higher EEA would result in hardship or an unfair loss." In the context of their proposal, Zhivan and others define "hardship" as difficulty working from ages 62 through 64 (which they assume is correlated with AIME level) and "unfairness" as the lower value of lifetime benefits that would be received by workers with below average life expectancy. As they note (2008, endnote 17), their proposal does not address the adequacy of benefit levels at age 62 for workers who are deemed eligible to claim at age 62. For example, under current law, when the FRA reaches 67, benefits received at age 62 will be 70 percent of benefits received at age 67 (Goss 2010). To address that automatic actuarial reduction, Zhivan and others further note that one option would be to fix the EEA benefit at 80 percent of the FRA benefit.27 In order to understand the distributional implications of their proposal, one must first understand differences in labor force participation between men and women and the limitations of Social Security's earnings data, which I review in the following section.
Differences in Hours Worked and Lifetime Earnings by Sex
The gradient analysis conducted on men in this article cannot be repeated for women because labor force attachment was not as strong for women as for men in the birth cohorts currently observable in Social Security data. For example, over the lifetime of these birth cohorts, average hours worked at the prime earnings ages of 25–54 grew from about 16 hours in 1968 to about 26 in the mid-1990s (and have since been steady) for women; those hours fell from about 40 in 1968 to 36 in the mid-1980s (and have since been steady) for men (Waldron 2012). As a result of differences in hours worked by sex, the male fully insured worker population recently eligible for retired-worker benefits is predominately composed of primary, full-time workers, while the female fully insured population includes a mix of primary, full-time workers and secondary, part-time workers (including workers with a large number of zero earning years relative to primary workers).
Social Security has no information on number of hours worked per year, on the reason a worker has years of zero earnings in their earnings record, or on marital status by year. Earnings are reported annually to Social Security's MEF on an individual basis with no marital information attached. I can only observe the lifetime earnings of a fully insured worker's spouse if one member of the couple has claimed auxiliary (that is, spouse or survivor) benefits based on the record of the highest earner in the couple.28 Such a sample would be skewed because an appropriate risk group should include all couples eligible to claim at a given age, not only all couples who have already claimed by a given age. Therefore, I am unable to create a measure of lifetime household earnings for fully insured workers using Social Security administrative data. For that reason, I cannot separate female primary earners from female secondary earners in my analysis. While as primary earners, men's lifetime earnings will be strongly correlated with their lifetime household income, and more broadly, their socioeconomic status, many female lifetime earners may have a weak correlation between their own lifetime earnings level and their lifetime household earnings and socioeconomic status.
As discussed, the lack of a household earnings measure is not a problem for men because, as the primary earner in the majority of households, their own earnings and their household earnings will be highly correlated in terms of their assignment to socioeconomic deciles. For women (particularly married women), their own lifetime earnings may serve as a poor proxy for their household earnings, so that the place of a woman in a socioeconomic decile based on her own earnings will not necessarily equal her place in a socioeconomic decile based on her household earnings. For example, Monk and others (2010) found that among individuals observed in the 1992–2006 Health and Retirement Survey, the highest AIME (a top 35-year lifetime earnings measure) in the household was a worker's own AIME for 97 percent of married men and only 15 percent of married women.
In addition, male lifetime earnings can capture causation running from poor health to lower earnings because low hours worked or periods of zero earnings are frequently correlated with a health shock or a chronic health problem for primary earners. For secondary earners (predominately women), zeroes and low hours worked can often signify participation in nonmarket work, such as childcare, for reasons uncorrelated with health. In other words, secondary earners with low hours worked and zero earnings for nonhealth reasons may be mixed in the same category with primary earners with low hours worked and zero earnings for health reasons to a much greater extent for women than for men, dampening the power of a lifetime earnings variable to explain mortality risk differences among women.
Recall that the AIME represents an average of a worker's top-35 years of earnings, while hardship is typically used to refer to the concept of household income, or the total resources available to an individual. As discussed, these two measures are unlikely to be as strongly correlated for women as for men because men work more market hours than women, on average, while women work more nonmarket hours than men, on average. Thus, while we would expect the female median AIME to move closer to the male AIME for more recent birth cohorts, given large increases in female labor force participation over time, it is not clear from the empirical data that the female AIME will equal the male AIME at the point at which a hypothetical proposed retired-worker law change is phased in. For example, women were still 23 percentage points below men in the number working full time, all year at the prime earnings ages in 2007 and were about 10 hours below men in average hours worked per week (Waldron 2012). Both of these trends have been flat for the past 10 years. From 2003 through 2007, among workers born in the 1970s, hours of paid work were about 41 for men and 26 for women, while hours of unpaid work were 16 for men and 32 for women (Krantz-Kent 2009), despite the fact that years of educational attainment were higher for women than for men in those birth cohorts. In addition, the Pew Research Center (2007) found that the preference for full-time work among fathers exceeded mothers by 50 percentage points in 2007, and that preference for part-time work differed little among mothers by education or income level. Finally, of people aged 15 or older who married during 2008 (the majority of whom were under age 35), 72 percent of men worked full time compared with only 50 percent of women (Kreider and Ellis 2011, Table 11).
Distributional Analysis of a Targeted Proposal by Sex
Although at various times throughout the history of the Social Security Act provisions have applied different rules to men and women, by 1983 the Social Security Act had once again been made gender neutral through both court decisions and legislative changes (Myers 1993).29 Despite that current-law gender neutrality, Zhivan and others (2008) seek to exploit known links between low lifetime earnings and high mortality risk for men as a way to target for relief fully insured workers in poorer health,30 if the EEA were to be increased. That proposal may miss its target by a wide margin if female life expectancy is higher than male life expectancy, but female lifetime earnings are lower. In the case of a policy option that links the EEA to AIME level, workers with higher life expectancy (women) could end up having a lower early retirement age than workers with lower life expectancy (men) by virtue of differences in earnings levels between men and women. In addition a secondary earner (such as a married women for whom hours of nonmarket work have exceeded hours of market work over a lifetime) could be more likely to qualify for a lower early retirement age based on her own retired-worker benefit than the equivalent primary earner who has worked full time at a modest hourly wage over a lifetime, even though her primary-earning counterpart could face a higher risk of death, be in poorer health, and have lower household income.31
Although this article examines the target efficiency of an EEA linked to AIME level by focusing on differences in lifetime earnings and mortality by sex, an additional concern discussed by Stapleton (2009, 25) is that an elastic EEA would not help workers who have high AIMEs but experience adverse health events. Support for that concern is found in Waldron (2004), where male Social Security retired-worker beneficiaries with earnings in the top quarter of the male lifetime earnings distribution who claimed at age 62 were found to have had poorer health and higher mortality risk than most men retiring at age 65, including those age-65 retirees with earnings in the lowest quartile. In other words, current-law equality in retirement ages by AIME provides insurance value against poor health at age 62, even for those at the top end of the earnings distribution, and there is evidence that some workers at the top end are making use of that insurance.
In order to examine the sensitivity of policy options that seek to mitigate the hardship caused by an EEA increase through the use of Social Security's AIME, I first tabulate relevant Social Security program variables by the male lifetime earnings deciles that I use to calculate mortality differentials in this analysis (Tables 3 and 4).32 Because there are large differences in lifetime earnings by sex that would be obscured by a unisex tabulation, I tabulate program variables separately by sex and use the male earnings distribution to assign women to earnings deciles. By assigning women in this way, I seek to roughly proxy for a primary or full-time worker definition when forming the earnings deciles. Because women have lower earnings than men, about 45 percent of female fully insured workers are in the bottom two male earnings deciles (Table 4). At the opposite end of the earnings distribution, only 0.6 percent of women are in the top male lifetime earnings decile.
| Male earnings decile | Median AIME | PIA a | Reduced monthly benefit amount at age 62 a | Benefit as a percentage of the 2002 poverty line for a one-person family | Percentage of men at or below 100 percent of the 2002 poverty line for a one-person family | Median years of Social Security– covered earnings at ages 14–61 | Percentage of earnings decile with disability insured status at age 61 | ||
|---|---|---|---|---|---|---|---|---|---|
| Median age-62 benefit a | Median age-62 benefit, if FRA was 67 a | At FRA of 65(6) b | At FRA of 67 | ||||||
| 1 | 1,008.00 | 665.92 | 516.09 | 70 | 63 | 87 | 92 | 21.0 | 25 |
| 2 | 1,667.50 | 876.96 | 679.64 | 92 | 83 | 62 | 76 | 32.3 | 73 |
| 3 | 2,259.50 | 1,066.40 | 826.46 | 112 | 101 | 31 | 48 | 38.5 | 88 |
| 4 | 2,821.00 | 1,246.08 | 965.71 | 131 | 118 | 10 | 16 | 40.8 | 89 |
| 5 | 3,304.00 | 1,400.64 | 1,085.50 | 147 | 133 | 7 | 8 | 41.3 | 89 |
| 6 | 3,704.00 | 1,505.35 | 1,166.65 | 158 | 143 | 10 | 11 | 41.5 | 88 |
| 7 | 4,173.00 | 1,575.70 | 1,221.17 | 165 | 149 | 10 | 11 | 41.3 | 86 |
| 8 | 4,653.00 | 1,647.70 | 1,276.97 | 173 | 156 | 8 | 8 | 41.8 | 89 |
| 9 | 5,100.00 | 1,714.75 | 1,328.93 | 180 | 163 | 7 | 8 | 41.5 | 91 |
| 10 | 5,366.00 | 1,754.65 | 1,359.85 | 184 | 166 | 3 | 4 | 40.8 | 95 |
| SOURCES: Author's calculations based on the Annual Statistical Supplement to the Social Security Bulletin, 2010 (Table 2.A17.1 and Table 3.E8.) and Social Security administrative data files (1 percent 2008 active CWHS, 1 percent 2009 MEF, 1 percent 2010 MBR, and 1 percent 2009 Numident). | |||||||||
| NOTES: Sample consists of men born in 1940 who were fully insured for retired-worker benefits; disabled-worker beneficiaries are excluded. Retired-worker benefits are reduced for an age-62 claim, based on the 1940 birth cohort's FRA of 65 years and 6 months. Earnings deciles are based on average relative earnings from ages 45 through 55. | |||||||||
| a. Author's calculations based on median AIME amount observed empirically. | |||||||||
| b. Age given in years and (months). | |||||||||
| Male earnings decile | Percentage of women in male earnings decile | Median AIME | PIA a | Reduced monthly benefit amount at age 62 a | Benefit as a percentage of the 2002 poverty line for a one-person family | Percentage of women at or below 100 percent of the 2002 poverty line for a one-person family | Median years of Social Security– covered earnings at ages 14–61 | Percentage of earnings decile with disability insured status at age 61 | ||
|---|---|---|---|---|---|---|---|---|---|---|
| Median age-62 benefit a | Median age-62 benefit, if FRA was 67 a | At FRA of 65(6) b | At FRA of 67 | |||||||
| 1 | 20.4 | 492.00 | 442.80 | 343.17 | 46 | 42 | 99 | 100 | 15.5 | 36 |
| 2 | 24.2 | 891.00 | 628.48 | 487.07 | 66 | 60 | 97 | 99 | 24.8 | 78 |
| 3 | 18.9 | 1,492.00 | 820.80 | 636.12 | 86 | 78 | 81 | 92 | 30.0 | 89 |
| 4 | 13.4 | 2,029.50 | 992.80 | 769.42 | 104 | 94 | 39 | 65 | 32.5 | 91 |
| 5 | 8.8 | 2,568.50 | 1,165.28 | 903.09 | 122 | 110 | 17 | 31 | 33.5 | 90 |
| 6 | 5.8 | 3,022.00 | 1,310.40 | 1,015.56 | 138 | 124 | 11 | 14 | 34.3 | 88 |
| 7 | 3.7 | 3,532.50 | 1,473.76 | 1,142.16 | 155 | 140 | 10 | 13 | 33.8 | 89 |
| 8 | 2.7 | 3,987.00 | 1,547.80 | 1,199.55 | 162 | 147 | 11 | 11 | 33.8 | 88 |
| 9 | 1.4 | 4,553.00 | 1,632.70 | 1,265.34 | 171 | 155 | 7 | 8 | 35.3 | 92 |
| 10 | 0.6 | 4,583.00 | 1,637.20 | 1,268.83 | 172 | 155 | 10 | 12 | 33.0 | 96 |
| SOURCES: Author's calculations based on the Annual Statistical Supplement to the Social Security Bulletin, 2010 (Table 2.A17.1 and Table 3.E8.) and Social Security administrative data files (1 percent 2008 active CWHS, 1 percent 2009 MEF, 1 percent 2010 MBR, and 1 percent 2009 Numident). | ||||||||||
| NOTES: Sample consists of women born in 1940 who were fully insured for retired-worker benefits; disabled-worker beneficiaries are excluded. Retired-worker benefits are reduced for an age-62 claim, based on the 1940 birth cohort's FRA of 65 years and 6 months. Earnings deciles are based on average relative earnings from ages 45 through 55. | ||||||||||
| a. Author's calculations based on median AIME amount observed empirically. | ||||||||||
| b. Age given in years and (months). | ||||||||||
After tabulating the median AIMEs by male earnings decile, I then calculate the median reduced monthly benefit at age 62 for a worker by earnings decile and the percentage of the poverty line such a median benefit represents. Because I cannot observe couples in my data, the poverty measure I use is equivalent to what a single worker would have faced.33 In reality, a married person could have received a spouse or widow benefit increment to the retired-worker benefit that is calculated in Tables 3 and 4 and that is payable on his or her own record).34 Because the 1940 birth cohort had a FRA of 65 years and 6 months and the FRA is scheduled under current law to increase to age 67 for birth cohorts 1960 and later, I also calculate the age-62 benefit as a percentage of the 2002 poverty line for one person by decile if the 1940 birth cohort had faced the benefit reductions scheduled under current law for the 1960 and later birth cohorts.
Retired-worker benefits reduced for an age-62 claim would have been around 100 percent of the poverty level at around the median of the 3rd male earnings decile for men and around the median of the 4th male earnings decile for women under the actual retirement age for the 1940 birth cohort, or closer to the median of the 5th male earnings decile for women if the retirement age had been 67 (see Tables 3 and 4). Aggregating across deciles (that is, multiplying the percentage of men or women in each male earnings decile with benefits at or below poverty by the percentage of all men or women in the decile, and adding up across deciles), I find that among fully insured workers at an FRA of 67, about 25 percent of men and 75 percent of women would have had a benefit at 100 percent of the poverty level or less. That difference by sex is driven by a lower median number of covered earnings years for women than men at every earnings decile. This does not mean that 75 percent of women in my sample are poor; such a conclusion is implausible and highlights the fact that female AIME levels are unlikely to correlate strongly with household income, poverty, or hardship measures for recently eligible birth cohorts.
We also see in Tables 3 and 4 that for both men and women there are smaller numbers of fully insured workers with AIMEs at or below the poverty level at higher earnings deciles. Some of those workers may have higher earnings that are not covered by Social Security and lower Social Security–covered earnings. Other workers may have emigrated from their native countries to the United States at later ages than the native born typically start working in covered employment.35 As Olsen and Hoffmeyer (2001/2002, 12) noted, even though the special minimum benefit (a retired-worker benefit originally designed to increase the benefit level of workers with low AIMEs) required 23 years of coverage, in 2000, 12 percent of retired-worker special minimum beneficiaries had income from noncovered pensions. The authors discussed the history of the special minimum, and Schobel and McKay (1982) discussed its predecessor—the regular minimum (another retired-worker benefit originally designed to increase the benefit level of workers with low AIMEs).
As discussed by Olsen and Hoffmeyer (2001/2002), in 1972 Congress rejected raising the level of the regular minimum benefit (which had fallen below the poverty line) because of concerns of windfalls going to workers who were only intermittently in Social Security–covered employment. The authors reported that the chief groups named in a 1972 Senate Finance Committee report consisted of workers employed either in the federal service, or under a state retirement system not linked to Social Security, or as a policeman or fireman, and women who spent "most of [their] adult [lives] not working but…had some earnings under Social Security" (5).36
Under the type of policy option we are analyzing here, workers with low Social Security–covered earnings and high earnings not covered by Social Security could be assigned an EEA of 62, while workers with a full employment history of lower Social Security–covered earnings could be assigned an EEA of 64, even though health and mortality risk may be expected to be worse for the latter group than for the former. In addition, the former group of workers may already have a state or local defined benefit pension plan with a low retirement age, while the latter may not.
Finally, we see in Tables 3 and 4 that if men with earnings in the bottom 30 percent of the male lifetime earnings distribution were assigned an EEA of 62 based on their AIME, about 64 percent of women would also have been assigned an EEA of 62. Conversely, many more men than women would have been assigned the highest EEA level designated in the policy option discussed by Zhivan and others (2008) by virtue of their higher AIMEs.
In order to test whether an EEA based on AIME level would correspond to observable differences in mortality risk between men and women by lifetime earnings decile, I calculate death rates for women classified by male earnings decile and compare them with male death rates classified by male earnings deciles (Chart 2). (The regression results from which the female death rates displayed in Chart 2 are calculated can be found in the Appendix (Tables A-5 and A-6).) If the policy option we are evaluating is designed to affect fully insured workers at a particular lifetime earnings level equally by sex, both men and women with equivalent lifetime earnings should have roughly equal death rates. As a further test, I also classify women into earnings deciles based on the female earnings distribution, although, as indicated in Chart 2, this results in little to no difference in the female death rates by decile. In neither case do we have a very strong measure of socioeconomic status for women; however, that is the point. SSA has never collected income data because income data is not used to administer the OASDI program. Because the Social Security retired-worker benefit was designed to be universal, it is extremely difficult to target subgroups efficiently through the retired-worker benefit.
Death rates by age, sex, and lifetime earnings deciles
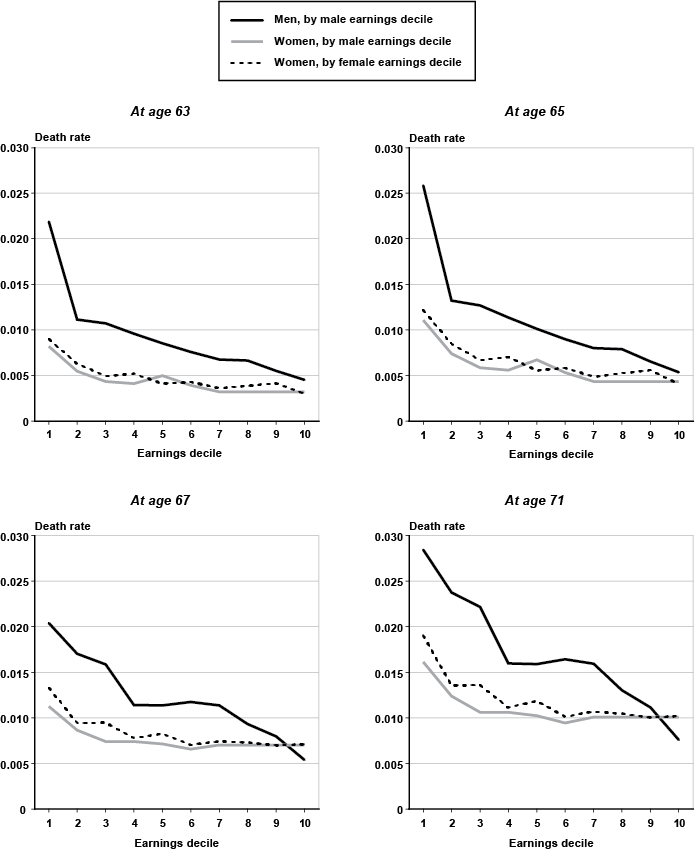
| Decile | Men, by male earnings decile | Women, by male earnings decile | Women, by female earnings decile |
|---|---|---|---|
| At age 63 | |||
| 1 | 0.022 | 0.008 | 0.009 |
| 2 | 0.011 | 0.005 | 0.006 |
| 3 | 0.011 | 0.004 | 0.005 |
| 4 | 0.010 | 0.004 | 0.005 |
| 5 | 0.009 | 0.005 | 0.004 |
| 6 | 0.008 | 0.004 | 0.004 |
| 7 | 0.007 | 0.003 | 0.004 |
| 8 | 0.007 | 0.003 | 0.004 |
| 9 | 0.006 | 0.003 | 0.004 |
| 10 | 0.005 | 0.003 | 0.003 |
| At age 65 | |||
| 1 | 0.026 | 0.011 | 0.012 |
| 2 | 0.013 | 0.007 | 0.009 |
| 3 | 0.013 | 0.006 | 0.007 |
| 4 | 0.011 | 0.006 | 0.007 |
| 5 | 0.010 | 0.007 | 0.006 |
| 6 | 0.009 | 0.005 | 0.006 |
| 7 | 0.008 | 0.004 | 0.005 |
| 8 | 0.008 | 0.004 | 0.005 |
| 9 | 0.007 | 0.004 | 0.006 |
| 10 | 0.005 | 0.004 | 0.004 |
| At age 67 | |||
| 1 | 0.020 | 0.011 | 0.013 |
| 2 | 0.017 | 0.009 | 0.009 |
| 3 | 0.016 | 0.007 | 0.009 |
| 4 | 0.011 | 0.007 | 0.008 |
| 5 | 0.011 | 0.007 | 0.008 |
| 6 | 0.012 | 0.007 | 0.007 |
| 7 | 0.011 | 0.007 | 0.007 |
| 8 | 0.009 | 0.007 | 0.007 |
| 9 | 0.008 | 0.007 | 0.007 |
| 10 | 0.005 | 0.007 | 0.007 |
| At age 71 | |||
| 1 | 0.028 | 0.016 | 0.019 |
| 2 | 0.024 | 0.012 | 0.014 |
| 3 | 0.022 | 0.011 | 0.014 |
| 4 | 0.016 | 0.011 | 0.011 |
| 5 | 0.016 | 0.010 | 0.012 |
| 6 | 0.016 | 0.009 | 0.010 |
| 7 | 0.016 | 0.010 | 0.011 |
| 8 | 0.013 | 0.010 | 0.010 |
| 9 | 0.011 | 0.010 | 0.010 |
| 10 | 0.008 | 0.010 | 0.010 |
As indicated in Chart 2, deaths rates for women are well below comparable male death rates at deciles 1 through 8 at ages 63–71. Men do not get close to the lower death rates of women in deciles 3 through 10 until about decile 9. Because we do not have a measure of income for women, it could well be that high-income women are well above the top 20 percent of male lifetime earners in terms of longevity. Nevertheless, with this major caveat in mind, we do have some evidence from Chart 2 that the top 20 percent of male lifetime earners could be close to the average woman in terms of mortality risk.
Until this point, I have not placed fully insured workers into deciles based on percentiles that are defined by the unisex (male and female combined) earnings distribution. Interpretation of estimates based on the unisex earnings distribution can be difficult, given the difference in hours worked between men and women and the fact that secondary workers in either a current marriage or in a marriage that has lasted at least 10 years may be dually entitled to Social Security spouse and survivor benefits (see Waldron (2012) for details). Nevertheless, retirement analysts sometimes classify workers by the unisex earnings distribution when presenting distributional results of analyses of proposed changes to retired-worker benefits.
In Table 5, I show the percentage of men and women born in 1940 who would have been in earnings deciles 1 through 10, using three different methods of calculating the earnings deciles. The first method uses the male earnings distribution to define the earnings deciles and places women in the male earnings deciles, based on their own lifetime earnings. Under this method, 44.6 percent of women have earnings in the bottom 20 percent of the male earnings distribution. The second method uses the female earnings distribution to define the earnings deciles and calculates the number of men who are in each female decile, based on their own lifetime earnings. Under this method, 9.9 percent of men have earnings in the bottom 20 percent of the female earnings decile. The third method uses the unisex earnings distribution to define lifetime earnings deciles and calculates the percentage of men and women in each earnings decile based on their own respective lifetime earnings. Under this method, 12.9 percent of men and 27.8 percent of women are in the bottom 20 percent of the unisex earnings distribution.
| Lifetime earnings decile | Women in male earnings decile | Men in female earnings decile | Women in unisex earnings decile | Men in unisex earnings decile |
|---|---|---|---|---|
| 1 | 20.4 | 5.7 | 13.3 | 7.0 |
| 2 | 24.2 | 4.2 | 14.5 | 5.9 |
| 3 | 18.9 | 3.9 | 14.3 | 6.2 |
| 4 | 13.4 | 4.4 | 14.0 | 6.4 |
| 5 | 8.8 | 4.4 | 12.4 | 7.8 |
| 6 | 5.8 | 5.3 | 11.1 | 9.0 |
| 7 | 3.7 | 6.7 | 8.5 | 11.4 |
| 8 | 2.7 | 8.4 | 6.4 | 13.3 |
| 9 | 1.4 | 13.9 | 3.9 | 15.5 |
| 10 | 0.6 | 43.2 | 1.7 | 17.5 |
| SOURCES: Author's calculations based on Social Security administrative data files (1 percent 2008 active CWHS, 1 percent 2009 MEF, 1 percent 2010 MBR, and 1 percent 2009 Numident). | ||||
| NOTE: Sample consists of men and women born in 1940 who were fully insured for retired-worker benefits; disabled-worker beneficiaries are excluded. | ||||
Table 5 can be used to roughly assess the target efficiency of a policy proposal that attempts to use Social Security's AIME as a way to shield workers in poor health from an increase in the EEA. For example, suppose a policy was to be designed to shield the bottom 20 percent of the unisex earnings distribution. Such a policy would have protected roughly 12.9 percent of men and 27.8 percent of women born in 1940. Table 6 displays the death rates at age 63 for men and women by male earnings decile. If policymakers used the 20 percent unisex distribution, they would have shielded women with death rates that ranged from roughly 0.008 to somewhere above 0.005. At that same point in the unisex distribution, they would have shielded men with death rates of roughly 0.022. The policy would have failed to shield men in deciles 2 through 5, all having higher death rates than the 27.8 percent of women who would have been shielded. In other words, at least 37 percent of men (50 minus 12.9) with death rates exceeding those of the women assigned the lowest EEA would have been assigned a higher EEA by the policy proposal.
| Male earnings decile | Percentage of women in male earnings decile | Death rate for— | |
|---|---|---|---|
| Men | Women | ||
| 1 | 20.4 | 0.021871 | 0.008184 |
| 2 | 24.2 | 0.011152 | 0.005467 |
| 3 | 18.9 | 0.010720 | 0.004335 |
| 4 | 13.4 | 0.009585 | 0.004136 |
| 5 | 8.8 | 0.008537 | 0.004974 |
| 6 | 5.8 | 0.007601 | 0.003941 |
| 7 | 3.7 | 0.006743 | 0.003213 |
| 8 | 2.7 | 0.006652 | 0.003213 |
| 9 | 1.4 | 0.005510 | 0.003213 |
| 10 | 0.6 | 0.004537 | 0.003213 |
| SOURCES: Author's calculations based on Social Security administrative data files (1 percent 2008 active CWHS, 1 percent 2009 MEF, 1 percent 2010 MBR, and 1 percent 2009 Numident). | |||
| NOTE: Sample consists of men and women born in 1940 who were fully insured for retired-worker benefits; disabled-worker beneficiaries are excluded. | |||
Alternatively, suppose policymakers chose to shield the bottom 20 percent of the male earnings distribution, recognizing that women live longer than men. At that point in the male earnings distribution, approximately 60 percent of men (80 minus 20) with death rates no lower than 0.007 would have had a higher EEA than the 44.6 percent of women in the bottom 20 percent of the male earnings distribution who would have had death rates of approximately 0.005. This analysis is exaggerated because we can expect younger female birth cohorts to have higher labor force participation, and thus higher lifetime earnings, than the 1940 birth cohort. However, as discussed, women are still 23 percentage points below men in the number working full time. Mathematically, lifetime earnings cannot become equal between the sexes if hours worked are unequal. (If women's wages exceeded men's wages by an enormous amount, such a result could be feasible; however, that particular scenario would be well outside the bounds of all existing empirical wage data.) Furthermore, female life expectancy at age 60 has been higher than male life expectancy at age 60 for at least a century.
As illustrated in Chart 2 and Tables 5 and 6, it would be difficult to focus retired-worker benefit changes on low earners with low life expectancy through a worker's own AIME because many women with higher life expectancy will qualify because of their relatively low AIME levels. Monk and others (2010) found similar results by sex when using a worker's own AIME quintile as a measure of socioeconomic status in a Health and Retirement Survey sample matched to Social Security administrative data. Specifically, they found, "while individual life expectancy is strongly correlated with individual AIME for men, it is only weakly correlated for women, and when pooling the genders the correlation disappears" (1).
Thus, given the higher labor force participation of men and greater number of hours worked, if one uses the unisex earnings distribution to define a low earner, many men at fairly high mortality risk relative to the total fully insured population will have an AIME level exceeding the AIME level specified in the policy option. On the other hand, if one uses the male earnings distribution to define a low earner, low-earning women may meet the AIME level specified for a particular benefit option, even though they appear likely to be in better health and have higher life expectancy than many of their male counterparts at equivalent or higher AIME levels.37
Distribution of Workers at the OASDI Taxable Maximum by Earnings Decile and Sex
In lieu of varying the EEA by AIME level, one way policymakers could focus on workers expected to have high life expectancy, while simultaneously including high-income but low-earnings workers, would be to increase the OASDI tax max. Unfortunately, this discussion is necessarily speculative, as we are not able to calculate the marriage rate for workers with earnings over the taxable maximum using Social Security data.
In theory, a Social Security policy change of this nature could indirectly apply to low-earning spouses of high-earning workers through the shared reduction in disposable income the couple would have experienced during the years at which the higher earner was paying taxes on a larger amount of earnings, relative to current law. With regard to life expectancy correlations, one advantage could be that, theoretically, low-earning, high-income workers could have fairly high life expectancy, perhaps even exceeding that of the higher earner in a high-income couple. An additional advantage could be that, under current law, unmarried workers are subject to the same payroll tax rate as married workers, but are not eligible for spouse or survivor benefits. While a universal tax rate applied to all Social Security–covered earnings hews to the universal principle underlying retired-worker benefit design, the payout of auxiliary benefits is not particularly progressive in outcome because married couples tend to have higher income than unmarried individuals.38
Gustman and Steinmeier (2001) and Gustman, Steinmeier, and Tabatabai (2011) observed within the Old-Age and Survivors Insurance system a large amount of redistribution from high-to-low-earning individuals and a much lesser amount of redistribution from high-to-low-earning households. In addition, for both men and women, marriage has been found to lower mortality risk, relative to the unmarried (Rendall and others 2011).
To examine the distributional effect of this hypothetical policy option, I next tabulate the percentage of men and women from ages 45 through 55 at the OASDI tax max (Table 7). At first glance, targeting the OASDI tax max for an increase appears to overshoot the target with regard to life expectancy for men and undershoot the target for women because about 35 percent of men had some earnings from ages 45 through 55 at the taxable maximum compared with only 7 percent of women.
| Number of years at OASDI tax max | Men | Women |
|---|---|---|
| 0 | 65.0 | 93.0 |
| 1 | 5.7 | 2.2 |
| 2 | 3.1 | 0.9 |
| 3 | 2.5 | 0.6 |
| 4 | 2.2 | 0.5 |
| 5 | 2.0 | 0.4 |
| 6 | 1.9 | 0.4 |
| 7 | 1.9 | 0.3 |
| 8 | 1.9 | 0.3 |
| 9 | 1.9 | 0.3 |
| 10 | 2.3 | 0.3 |
| 11 | 9.7 | 0.8 |
| SOURCES: Author's calculations based on Social Security administrative data files (1 percent 2008 active CWHS, 1 percent 2009 MEF, 1 percent 2010 MBR, and 1 percent 2009 Numident). | ||
| NOTE: Sample consists of men and women born in 1940 who were fully insured for retired-worker benefits; disabled-worker beneficiaries are excluded. | ||
However, if we examine the median number of years at the OASDI tax max (out of a possible 11) in Table 8, we see that the majority of the tax increase will fall on male earnings deciles 9 and 10. Decile 8 only has a median 2 years out of a possible 11 at the OASDI tax max, and all deciles below 8 had a median of zero years at the OASDI tax max. Thus, the majority of the tax increase is likely to fall on men closest to the observable threshold, the top 20 percent of the male earnings distribution. (Although, because, at least at ages 67–71, the threshold is actually at the top 5–10 percent of the male earnings distribution for men, this option may tend to hit the 9th decile harder than the 10th decile.)
| Male earnings decile | Men | Women |
|---|---|---|
| 1 | 0 | 0 |
| 2 | 0 | 0 |
| 3 | 0 | 0 |
| 4 | 0 | 0 |
| 5 | 0 | 0 |
| 6 | 0 | 0 |
| 7 | 0 | 0 |
| 8 | 2 | 2 |
| 9 | 9 | 8 |
| 10 | 11 | 11 |
| SOURCES: Author's calculations based on Social Security administrative data files (1 percent 2008 active CWHS, 1 percent 2009 MEF, 1 percent 2010 MBR, and 1 percent 2009 Numident). | ||
| NOTE: Sample consists of men and women born in 1940 who were fully insured for retired-worker benefits; disabled-worker beneficiaries are excluded. | ||
On the other hand, there remains the problem of a potential undershooting of the target for women. In terms of a women's own earnings, death rates appear flat starting in the 3rd male lifetime earnings decile (or for the top 55 percent of female earners), and only 2 percent of women were in the top-two male earnings deciles in 2002. Even if we take the extreme assumption that 100 percent of men at the OASDI tax max are married, there may still be long-lived women married to men earning below the OASDI tax max who are not "paying" the full price of their longevity.
If policymakers wish to "charge" these women, one option could be to focus on survivors benefits. In 2009, for example, 98.5 percent of nondisabled widow(er) benefits were paid to women (SSA 2011, Table 5.F8). On the other hand, while this type of target would be more directly aimed at the longest lived of fully insured workers, reductions to survivor benefits may also be more likely to increase the poverty rates of women at older ages, relative to current law. If we consider that the Social Security retired-worker benefit is intended to provide longevity insurance, then reducing the benefits of the longest-lived beneficiaries could be counterproductive.
For this reason, an increase in the OASDI tax max would tend to preserve longevity insurance more than a survivor or retired-worker benefit reduction,39 while still focusing on fairly long-lived individuals relative to the total fully insured population. In other words, those fully insured (male) workers who are expected to collect Social Security benefits over a longer period of time, relative to other fully insured (male) workers, would be those asked to pay more for their insurance, relative to current law. However, a remaining empirical question concerns how fair such an option would be for unmarried men with earnings above the OASDI tax max, who might have higher mortality risk than some lower-earning women, but who would not have a spouse who would collect survivor's insurance on their earnings record upon their death. Those unmarried men would receive less insurance coverage for an equivalent level of tax contributions, relative to their married counterparts.
Conclusion
I have used a simple and clean measure of health (mortality) and a standardized measure of financial condition (position in the lifetime earnings distribution) to test the hypothesis that poor health and mortality among older men follows a poverty threshold model. Using Social Security administrative data, I found that among men ages 63–71 the point above which differences in mortality risk by earnings become undetectable is somewhere in the top 20 percent of the male lifetime earnings distribution. In other words, fully insured men in at least the bottom 80 percent of the lifetime earnings distribution exhibited a negative correlation with mortality (the higher the earnings, the lower the mortality risk).
The Social Security administrative data strongly reject the poverty threshold model, a result similar to results found for Canada, Germany, and England. Analyses using a threshold model, by assuming that everyone above some point low in the earnings distribution has equal health and mortality prospects, will produce distributional estimates that will vary from the true distributional effects by a potentially large, unknown, and unmeasured margin. In addition, policymakers may be unaware of the uncertainty inherent in estimates produced from hardship threshold models because there is no good way to calculate an uncertainty band around an analyst's judgment of what constitutes hardship for a fully insured worker. In contrast, with gradient models analysts can employ standard statistical techniques for estimating uncertainty around point estimates.
Because the Social Security retired-worker benefit was designed to be universal, it is extremely difficult to target subgroups effectively through the retired-worker benefit. For example, we have seen that, on average, the longest-lived workers (women) have the lowest earnings and hours worked. Thus, a worker's own AIME would be a poor target, if one's goal is to shield or protect those workers who are the most likely to have adverse health and mortality characteristics. Such a target could potentially shield more advantaged women, while failing to shield less advantaged men. More broadly, we have found that, among men, there is no statistically significant low hardship threshold that exists between those who are in adverse circumstances and those who are not, when mortality risk is used as a measure of hardship.
Under current law, the link between earnings and benefit levels and the equal application of age-of-entitlement rules, regardless of earnings levels, means that a worker is never penalized for additional work or thrift. Because the insured population does not fall neatly into a low-earnings poor health group and a remaining good health group, attempts to target a subset of badly disadvantaged workers by altering the benefit rules that apply equally to everyone could both miss the intended target and introduce work disincentives into a program currently designed to reward work.
Appendix
Death rates for fully insured men born in 1940, by age and male lifetime earnings decile: Restricted analytical sample
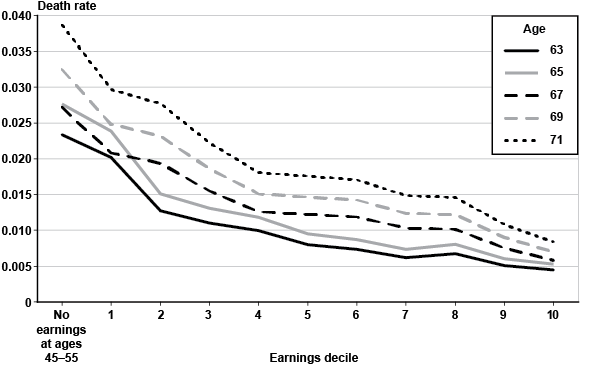
| Decile | Age 63 | Age 65 | Age 67 | Age 69 | Age 71 |
|---|---|---|---|---|---|
| No earnings from ages 45–55 | 0.023 | 0.028 | 0.027 | 0.033 | 0.039 |
| 1 | 0.020 | 0.024 | 0.021 | 0.025 | 0.030 |
| 2 | 0.013 | 0.015 | 0.019 | 0.023 | 0.028 |
| 3 | 0.011 | 0.013 | 0.016 | 0.019 | 0.022 |
| 4 | 0.010 | 0.012 | 0.013 | 0.015 | 0.018 |
| 5 | 0.008 | 0.010 | 0.012 | 0.015 | 0.018 |
| 6 | 0.007 | 0.009 | 0.012 | 0.014 | 0.017 |
| 7 | 0.006 | 0.007 | 0.010 | 0.012 | 0.015 |
| 8 | 0.007 | 0.008 | 0.010 | 0.012 | 0.015 |
| 9 | 0.005 | 0.006 | 0.008 | 0.009 | 0.011 |
| 10 | 0.005 | 0.005 | 0.006 | 0.007 | 0.008 |
| Variable | Ages 63–66 | Ages 67–71 | ||
|---|---|---|---|---|
| Parameter estimate | Standard error | Parameter estimate | Standard error | |
| Intercept | 21.6142 | 16.7488 | 80.0712 | 43.1339*** |
| Age | 0.0856 | 0.0173* | 0.0851 | 0.0210* |
| Year of birth | -0.0167 | 0.00847** | -0.0469 | 0.0219** |
| Decile | ||||
| 1 | 1.5905 | 0.0919* | 1.3410 | 0.1208* |
| 2 | 0.9061 | 0.0990* | 1.1572 | 0.1226* |
| 3 | 0.8661 | 0.0996* | 1.0862 | 0.1235* |
| 4 | 0.7531 | 0.1013* | 0.7522 | 0.1294* |
| 5 | 0.6362 | 0.1032* | 0.7473 | 0.1294* |
| 6 | 0.5192 | 0.1054* | 0.7816 | 0.1286* |
| 7 | 0.3985 | 0.1078* | 0.7486 | 0.1291* |
| 8 | 0.3848 | 0.1081* | 0.5459 | 0.1336* |
| 9 | 0.1954 | 0.1125*** | 0.3870 | 0.1375** |
| -2Log likelihood | 31885.038 | 19537.190 | ||
| SOURCES: Author's calculations based on Social Security administrative data files (1 percent 2008 active CWHS, 1 percent 2009 MEF, 1 percent 2010 MBR, and 1 percent 2009 Numident). | ||||
| NOTES: At ages 63–66, N = 277,024 pooled observations and 2,936 deaths. At ages 67–71, N = 120,203 pooled observations and 1,934 deaths.
Sample consists of men born from 1937 through 1945 who were fully insured for retired-worker benefits; disabled-worker beneficiaries are excluded. Reference variable is decile 10 (average relative earnings from ages 45 through 55 in the 91st–100th percentile of the earnings distribution).
* = significant at the 1 percent level; ** = significant at the 5 percent level; *** = significant at the 10 percent level.
|
||||
| Variable | Ages 63–66 | Ages 67–71 | ||
|---|---|---|---|---|
| Parameter estimate | Standard error | Parameter estimate | Standard error | |
| Intercept | 21.6635 | 16.7490 | 79.8291 | 43.1355*** |
| Age | 0.0856 | 0.0173* | 0.0852 | 0.0210* |
| Year of birth | -0.0167 | 0.00847** | -0.0469 | 0.0219** |
| Decile | ||||
| 1 | 1.5414 | 0.1214* | 1.6263 | 0.1816* |
| 2 | 0.8570 | 0.1269* | 1.4425 | 0.1828* |
| 3 | 0.8170 | 0.1274* | 1.3715 | 0.1834* |
| 4 | 0.7040 | 0.1287* | 1.0375 | 0.1874* |
| 5 | 0.5871 | 0.1302* | 1.0326 | 0.1874* |
| 6 | 0.4701 | 0.1319* | 1.0670 | 0.1869* |
| 7 | 0.3494 | 0.1339* | 1.0339 | 0.1873* |
| 8 | 0.3357 | 0.1341** | 0.8313 | 0.1904* |
| 9 | 0.1463 | 0.1377 | 0.6723 | 0.1931* |
| 91st–95th earnings percentile | -0.1005 | 0.1667 | 0.5082 | 0.2182** |
| -2Log likelihood | 31884.674 | 19531.594 | ||
| SOURCES: Author's calculations based on Social Security administrative data files (1 percent 2008 active CWHS, 1 percent 2009 MEF, 1 percent 2010 MBR, and 1 percent 2009 Numident). | ||||
| NOTES: At ages 63–66, N = 277,024 pooled observations and 2,936 deaths. At ages 67–71, N = 120,203 pooled observations and 1,934 deaths.
Sample consists of men born from 1937 through 1945 who were fully insured for retired-worker benefits; disabled-worker beneficiaries are excluded. Reference variable is average relative earnings from ages 45 through 55 in the 96th–100th percentile of the earnings distribution.
* = significant at the 1 percent level; ** = significant at the 5 percent level; *** = significant at the 10 percent level.
|
||||
| Variable | Ages 63–66 | Ages 67–71 | ||
|---|---|---|---|---|
| Parameter estimate | Standard error | Parameter estimate | Standard error | |
| Intercept | 22.7913 | 18.0482 | 82.0620 | 46.1325*** |
| Age | 0.0853 | 0.0186* | 0.0914 | 0.0224* |
| Year of birth | -0.0173 | 0.00913*** | -0.0481 | 0.0234** |
| No earnings at ages 45–55 | 1.6669 | 0.1251* | 1.5527 | 0.1643* |
| Decile | ||||
| 1 | 1.5166 | 0.1025* | 1.2777 | 0.1298* |
| 2 | 1.0514 | 0.1077* | 1.2061 | 0.1303* |
| 3 | 0.9062 | 0.1098* | 0.9819 | 0.1339* |
| 4 | 0.8042 | 0.1114* | 0.7699 | 0.1379* |
| 5 | 0.5867 | 0.1154* | 0.7418 | 0.1383* |
| 6 | 0.4975 | 0.1172* | 0.7119 | 0.1388* |
| 7 | 0.3260 | 0.1212* | 0.5719 | 0.1420* |
| 8 | 0.4165 | 0.1191* | 0.5531 | 0.1426* |
| 9 | 0.1284 | 0.1266 | 0.2506 | 0.1509** |
| -2Log likelihood | 27280.045 | 16896.228 | ||
| SOURCES: Author's calculations based on Social Security administrative data files (1 percent 2008 active CWHS, 1 percent 2009 MEF, 1 percent 2010 MBR, and 1 percent 2009 Numident). | ||||
| NOTES: At ages 63–66, N = 230,586 pooled observations and 2,533 deaths. At ages 67–71, N = 99,504 pooled observations and 1,696 deaths.
Sample consists of men born from 1937 through 1945 who were fully insured for retired-worker benefits; disabled-worker beneficiaries, the foreign born, and workers with mostly non–OASDI taxable earnings are excluded. Reference variable is decile 10 (average relative earnings from ages 45 through 55 in the 91st–100th percentile of the earnings distribution). The age 45–55 measure includes nonzero earnings only.
* = significant at the 1 percent level; ** = significant at the 5 percent level; *** = significant at the 10 percent level.
|
||||
| Variable | Decile 2 | Decile 3 | Decile 4 | Decile 5 | Decile 6 | Decile 7 | Decile 8 | Decile 9 | Decile 10 |
|---|---|---|---|---|---|---|---|---|---|
| Fully insured men aged 63–66 | |||||||||
| Decile 1 | 1.59* | 1.84* | 2.04* | 2.53* | 2.77* | 3.29* | 3.00* | 4.01* | 4.56* |
| (1.39–1.83) | (1.59–2.13) | (1.75–2.37) | (2.16–2.98) | (2.35–3.27) | (2.76–3.93) | (2.53–3.57) | (3.31–4.85) | (3.73–5.57) | |
| Decile 2 | 1.16*** | 1.28** | 1.59* | 1.74* | 2.07* | 1.89* | 2.52* | 2.86* | |
| (0.99–1.36) | (1.09–1.51) | (1.34–1.89) | (1.46–2.08) | (1.71–2.49) | (1.57–2.27) | (2.06–3.08) | (2.32–3.53) | ||
| Decile 3 | 1.11 | 1.38** | 1.50* | 1.79* | 1.63* | 2.18* | 2.48* | ||
| (0.94–1.31) | (1.15–1.65) | (1.25–1.81) | (1.47–2.17) | (1.35–1.97) | (1.77–2.67) | (2.00–3.07) | |||
| Decile 4 | 1.24** | 1.36** | 1.61* | 1.47* | 1.97* | 2.24* | |||
| (1.04–1.49) | (1.13–1.64) | (1.33–1.96) | (1.22–1.78) | (1.59–2.42) | (1.80–2.78) | ||||
| Decile 5 | 1.09 | 1.30** | 1.19** | 1.58* | 1.80* | ||||
| (0.90–1.33) | (1.06–1.59) | (0.97–1.45) | (1.27–1.97) | (1.43–2.26) | |||||
| Decile 6 | 1.19 | 1.08 | 1.45** | 1.65* | |||||
| (0.97–1.46) | (0.88–1.33) | (1.16–1.80) | (1.31–2.07) | ||||||
| Decile 7 | 0.91 | 1.22*** | 1.39** | ||||||
| (0.74–1.13) | (0.97–1.53) | (1.09–1.76) | |||||||
| Decile 8 | 1.33** | 1.52* | |||||||
| (1.07–1.67) | (1.20–1.92) | ||||||||
| Decile 9 | 1.14 | ||||||||
| (0.89–1.46) | |||||||||
| Fully insured men aged 67–71 | |||||||||
| Decile 1 | 1.07 | 1.34* | 1.66* | 1.71* | 1.76* | 2.03* | 2.06* | 2.79* | 3.59* |
| (0.90–1.28) | (1.11–1.62) | (1.36–2.03) | (1.40–2.09) | (1.44–2.16) | (1.64–2.50) | (1.67–2.55) | (2.21–3.53) | (2.78–4.63) | |
| Decile 2 | 1.25** | 1.55* | 1.59* | 1.64* | 1.89* | 1.92* | 2.60* | 3.34* | |
| (1.04–1.51) | (1.27–1.89) | (1.30–1.95) | (1.34–2.01) | (1.53–2.33) | (1.55–2.38) | (2.06–3.28) | (2.59–4.31) | ||
| Decile 3 | 1.24** | 1.27** | 1.31** | 1.51* | 1.54* | 2.08* | 2.67* | ||
| (1.00–1.52) | (1.03–1.57) | (1.06–1.62) | (1.21–1.88) | (1.23–1.92) | (1.63–2.64) | (2.05–3.47) | |||
| Decile 4 | 1.03 | 1.06 | 1.22*** | 1.24*** | 1.68* | 2.16* | |||
| (0.83–1.28) | (0.85–1.32) | (0.97–1.53) | (0.99–1.56) | (1.31–2.16) | (1.65–2.83) | ||||
| Decile 5 | 1.03 | 1.19 | 1.21 | 1.63* | 2.10* | ||||
| (0.82–1.29) | (0.94–1.49) | (0.96–1.52) | (1.27–2.10) | (1.60–2.75) | |||||
| Decile 6 | 1.15 | 1.17 | 1.59* | 2.04* | |||||
| (0.91–1.45) | (0.93–1.48) | (1.23–2.04) | (1.55–2.67) | ||||||
| Decile 7 | 1.02 | 1.38** | 1.77* | ||||||
| (0.80–1.30) | (1.06–1.79) | (1.34–2.34) | |||||||
| Decile 8 | 1.35** | 1.74* | |||||||
| (1.04–1.75) | (1.31–2.30) | ||||||||
| Decile 9 | 1.28*** | ||||||||
| (0.96–1.73) | |||||||||
| SOURCES: Author's calculations based on Social Security administrative data files (1 percent 2008 active CWHS, 1 percent 2009 MEF, 1 percent 2010 MBR, and 1 percent 2009 Numident). | |||||||||
| NOTES: Sample consists of men born from 1937 through 1945 who were fully insured for retired-worker benefits; disabled-worker beneficiaries, the foreign born, and workers with mostly non-Social Security–covered work from ages 45 through 55 are excluded.
* = significant at the 1 percent level; ** = significant at the 5 percent level; *** = significant at the 10 percent level.
|
|||||||||
| Variable | Percentage of women in male earnings decile | Ages 63–66 | Ages 67–71 | ||
|---|---|---|---|---|---|
| Parameter estimate | Standard error | Parameter estimate | Standard error | ||
| Intercept | . . . | 37.0857 | 23.4664 | 30.6624 | 56.0571 |
| Age | . . . | 0.1517 | 0.0239* | 0.0910 | 0.0273* |
| Year of birth | . . . | -0.0270 | 0.0119* | -0.0215 | 0.0284 |
| Male earnings decile | |||||
| 1 | 21 | 0.9399 | 0.1215** | 0.4744 | 0.1326* |
| 2 | 24 | 0.5336 | 0.1241* | 0.2091 | 0.1349 |
| 3 | 19 | 0.3004 | 0.1308** | 0.0534 | 0.1415 |
| 4 | 13 | 0.2532 | 0.1387*** | 0.0502 | 0.1496 |
| 5 | 9 | 0.4386 | 0.1455* | 0.0139 | 0.1660 |
| 6 | 6 | 0.2048 | 0.1693 | -0.0648 | 0.1937 |
| -2Log likelihood | . . . | 18397.649 | 12628.908 | ||
| SOURCES: Author's calculations based on Social Security administrative data files (1 percent 2008 active CWHS, 1 percent 2009 MEF, 1 percent 2010 MBR, and 1 percent 2009 Numident). | |||||
| NOTES: At ages 63–66, N = 254,943 pooled observations and 1,519 deaths. Sample consists of women born from 1937 through 1945 who were fully insured for retired-worker benefits; disabled-worker beneficiaries are excluded.
At ages 67–71, N = 111,486 pooled observations and 1,137 deaths. Sample consists of women born from 1937 through 1941 who were fully insured for retired-worker benefits; disabled-worker beneficiaries are excluded.
Reference variable is average relative earnings from ages 45 through 55 in the 61st–100th percentile of the male earnings distribution (9.2 percent of the female sample).
. . . = not applicable.
* = significant at the 1 percent level; ** = significant at the 5 percent level; *** = significant at the 10 percent level.
|
|||||
| Variable | Ages 63–66 | Ages 67–71 | ||
|---|---|---|---|---|
| Parameter estimate | Standard error | Parameter estimate | Standard error | |
| Intercept | 53.3196 | 23.4372** | 45.0153 | 56.0366 |
| Age | 0.1517 | 0.0239* | 0.0912 | 0.0273* |
| Year of birth | -0.0354 | 0.0119* | -0.0289 | 0.0284 |
| Female earnings decile | ||||
| 1 | 1.0988 | 0.1191* | 0.6336 | 0.1273* |
| 2 | 0.7384 | 0.1252* | 0.2878 | 0.1355** |
| 3 | 0.4945 | 0.1306* | 0.2905 | 0.1353** |
| 4 | 0.5452 | 0.1294* | 0.0898 | 0.1415 |
| 5 | 0.3100 | 0.1355** | 0.1525 | 0.1394 |
| 6 | 0.3530 | 0.1342* | -0.00822 | 0.1446 |
| 7 | 0.1744 | 0.1395 | 0.0469 | 0.1425 |
| 8 | 0.2521 | 0.1371*** | 0.0274 | 0.1432 |
| 9 | 0.3162 | 0.1353** | -0.0145 | 0.1450 |
| -2Log likelihood | 18376.361 | 12619.283 | ||
| SOURCES: Author's calculations based on Social Security administrative data files (1 percent 2008 active CWHS, 1 percent 2009 MEF, 1 percent 2010 MBR, and 1 percent 2009 Numident). | ||||
| NOTES: At ages 63–66, N = 254,943 pooled observations and 1,519 deaths. Sample consists of women born from 1937 through 1945 who were fully insured for retired-worker benefits; disabled-worker beneficiaries are excluded.
At ages 67–71, N = 111,486 pooled observations and 1,137 deaths. Sample consists of women born from 1937 through 1941 who were fully insured for retired-worker benefits; disabled-worker beneficiaries are excluded.
Reference variable is decile 10 (average relative earnings from ages 45 through 55 in the 91st–100th percentile of the female earnings distribution).
* = significant at the 1 percent level; ** = significant at the 5 percent level; *** = significant at the 10 percent level.
|
||||
Notes
1 It is difficult to determine empirically if the underlying data itself changed from following a poverty threshold model to a gradient model or if the gradient model always existed, but was not observable because of a lack of detailed data. In other words, one cannot generally go back in time and replicate older studies using newer models because the older data are too heavily top coded, censored, or otherwise limited, compared with the more recent data. There may be some evidence for the idea that health and mortality have always followed a gradient in the writings of the 1935 Committee on Economic Security, who designed Social Security's old-age (retired worker) insurance benefit (Project on the Federal Social Role 1985). See this article's companion piece (Waldron, forthcoming) for details.
2 Kitagawa and Hauser (1973) were unable to perform as strong a test of the gradient hypothesis because their data were more limited.
3 The following discussion refers to studies that are limited to observable empirical data. Distributional evaluations of proposed Social Security law changes that are based on the projections of microsimulation models, such as the Social Security Administration's Modeling Income in the Near Term (MINT) and the Urban Institute's Dynasim model, regularly present results using a variety of quintile measures. For an example of a MINT evaluation of a proposed increase in Social Security's full retirement age, see Springstead (2011).
4 For a review of 27 separate studies in which self-reported health is tested and found to be a predictor of mortality, see Idler and Benyamini (1997).
5 Social Security's retired-worker benefit has three key ages: the age at which a worker is first eligible to claim retired-worker benefits (the EEA—currently age 62); the age at which a worker can claim retired-worker benefits without an actuarial reduction for early retirement (the full retirement age (FRA)—currently age 66, rising to age 67 under current law); and the age beyond which extra credits are not given to workers who claim after the FRA (the delayed retirement credit age—currently age 70). Under current law, retired-worker monthly benefit amounts are reduced for retirement prior to the FRA. When the FRA reaches 67 as scheduled under current law for those born in 1960 or later, benefits received at age 62 will be 70 percent of benefits received at age 67 (Goss 2010). (See also http://www.socialsecurity.gov/retire2/agereduction.htm). Because benefits are actuarially reduced for workers who claim prior to the FRA, an increase in the EEA would cause a larger benefit to be available for a shorter period of time, rather than a smaller benefit to be available for a longer period of time, and, on average, such an increase would have no effect on the long-range financial status of the Social Security trust funds. In contrast, an increase in the FRA would be a reduction in future scheduled benefits relative to current law. Note that because benefits are actuarially reduced for early retirement, if the FRA is increased beyond age 67, benefits received at age 62 will be automatically reduced by an amount greater than the 30 percent reduction scheduled to take place when the retirement age reaches 67.
6 I am measuring correlation, not causation in this article. From a life-course perspective, causation can flow from both health to earnings and earnings to health and may begin in childhood or even in utero based on the socioeconomic status of one's parents or guardians.
7 Duleep (1986), in turn, was preceded by Caldwell and Diamond (1979) and Rosen and Taubman (1979). Those 1979 papers presented estimates at ages 65 plus, but the set up of the analyses with regard to the age of observation of the earnings and construction of the earnings categories precludes direct comparison with this work. More recently, Duggan, Gillingham, and Greenlees (2007) used the Continuous Work History Sample (capped taxable earnings and lump-sum earnings from 1937 through 1950) and found that mortality was negatively related to lifetime earnings (the higher the mortality, the lower the lifetime earnings) among Social Security retired-worker beneficiaries. However, they did not explicitly test the shape of the relationship between lifetime earnings and mortality, so results are not directly comparable to those found here.
8 Wolfson and others (1993) found that the bottom earnings percentile (the bottom 9 percent of the earnings distribution) did not follow this pattern; mortality risk for this group was lower than for higher groups. The authors stated that individuals in this group may have had unobservable (non-Canadian Pension Plan contributable) income. The description of Wolfson and others (1993) results described in this study is based on a conservative interpretation of Figure 2 (S172) in their analysis. In the text (S171), Wolfson and others stated that they observed "higher income males experienced lower mortality all the way up to the top 2 percent of the population"; however, that result does not appear to be explicitly depicted in Figure 2.
9 Quintile 1 experiences lower mortality risk than quintile 2, but the authors noted that this was due to low observed earnings and high unobserved earnings for many men in this category whose lifetime earnings were only partially covered under the German pension system (for example, civil servants).
10 The term "active" means that an individual had to have had at least one earnings report from 1951 through 2008 to be included in the 2008 active CWHS.
11 Technically, this type of earnings data exists in the MEF beginning in 1978, but non-OASDI taxable earnings data from 1978 through 1981 are subject to reporting errors and are not used in this analysis.
12 It is possible that a worker becomes entitled to a disabled-worker benefit, recovers, and then later becomes "newly eligible" for a retired-worker benefit. That population, which is expected to be small, is deleted under my methodology.
13 In other words, all workers observed are equally exposed to the risk of claiming benefits at age 62. That restriction will be more important for future work examining benefit claiming by lifetime earnings decile. It is made here, in part, to enable easier comparisons across work. Workers who die in the year in which they attain age 62 can also be affected by proposals to raise the EEA, to the extent that they survive long enough to collect benefits for the months after their retired-worker claim but before death, although they are excluded from my sample. All workers who die at age 63 or later would be potentially affected by an increase in the EEA because they would have had at least 1 less year (that is, age 62) over which to collect their retired-worker benefits.
14 SSA (2011, D.2).
15 See http://www.socialsecurity.gov/oact/COLA/Benefits.html#aime.
16 Under current law, the minimum number of years of earnings required to become fully insured for Social Security worker benefits for those born in 1929 or later is 10 years (40 quarters of coverage).
17 As described in the 2010 OASDI Trustees Report, Social Security's AWI is "a series that generally increases with the average amount of total wages for each year after 1950, including wages in noncovered employment and wages in covered employment in excess of the OASDI contribution and benefit base" (Board of Trustees 2010). Wage indexing brings nominal wages in a person's earnings record up to near-current wage levels. Wages are always indexed to the year that comes 2 years prior to the year of first eligibility. For example, for a worker retiring in 2011, wages would by indexed to the AWI for 2009. As described at http://www.socialsecurity.gov/OACT/ProgData/retirebenefit1.html, a factor will always equal 1 for the year in which the person attains age 60 and all later years. The indexing factor for a prior year Y is the result of dividing the AWI for the year in which the person attains age 60 by the AWI for year Y.
18 For example, for an individual who first becomes eligible for Old-Age Insurance benefits or Disability Insurance benefits in 2013, his or her PIA will be the sum of (a) 90 percent of the first $791 of his or her AIME; plus (b) 32 percent of his or her AIME over $791 and through $4,768; plus (c) 15 percent of his or her AIME over $4,768.
20 The sample is restricted to individuals who had survived to at least age 63 before calculating average earnings, so that each decile contains 10 percent of the sample in the year individuals were newly eligible for Social Security retired-worker benefits. (The force of differential mortality will cause the number of people in deciles calculated at any given age to eventually decline more at the bottom than the top of the deciles, as the sample population ages.) While wage earnings are recorded in the MEF over the OASDI taxable maximum beginning in 1982, self-employment earnings are reported only up to Medicare's Hospital Insurance (HI) taxable maximum prior to 1994. (The HI taxable maximum was the same as the OASDI taxable maximum from 1982 through 1990. Separate HI taxable maximums of $125,000; $130,200; and $135,000 applied from 1991 through 1993, respectively. The HI taxable maximum was eliminated in 1994.) A small number of individuals have earnings capped at the HI taxable maximum from 1982 through 1993 (ranging from 0.45 percent of the sample in 1982, to 2.2 percent in 1990, to 0.6 percent in 1993). Earnings for those individuals are imputed with a tobit regression prior to averaging. See Pattison and Waldron (2008) for more details on MEF earnings. For details on the tobit regression, see Waldron (2004, Appendix).
21 For example, it is not clear that a college student working part time is a "low earner" in the same way that a man with low earnings at age 50 is a low earner. Many young workers may have high earnings potential; in contrast, by the peak of the age-earner profile, adult socioeconomic status is essentially set. Earnings after the peak are problematic because some workers may retire early with pensions and still be healthy and of high income. A zero in the earnings record because of voluntary retirement would not be equivalent to a zero that is due to an unemployment or health shock, but we have no way of distinguishing between the two zeroes in Social Security data.
22 Year of death is the most robust unit of measurement. Month and day of death are less reliable. Greater detail in the timing of death is not really necessary for the purposes of this analysis.
23 The implication of this assumption is that when two or more events appear to happen at the same time (that is, are tied), there is no underlying ordering; rather, the events really happened at the same time (Allison 1995, 134).
24 Although the point estimate on the odds ratio is statistically significant at the 10 percent level when we compare the odds of death for decile 9 with those for decile 10 at ages 63–66, note that the confidence interval crosses 1 (Table 1). On the other hand, the pattern of the decline in odds ratios follows a clear gradient for deciles 1 through 8 versus decile 10 (last column in Table 1), and the point estimate on decile 9 plausibly follows that pattern. In conclusion, the exact location of the threshold is somewhat ambiguous; the most conservative interpretation would be that the threshold is no lower than the 9th decile (the top 20 percent of the male lifetime earnings distribution).
25 In results not shown, the 96th–97th percentile of the male lifetime earnings distribution did not have significantly higher mortality risk than the 98th–100th percentile of the earnings distribution at ages 67–71. As shown in the Appendix, Table A-2, the 91st–95th percentile of the earnings distribution had significantly higher mortality risk than the 96th–100th percentile of the earnings distribution at ages 67–71, but not at ages 63–66. Thus, the top 5 percent of the earnings distribution was homogenous with respect to mortality risk at ages 67–71.
26 As a side note, some retirement researchers erroneously believe that because less-educated workers enter the labor force at younger ages, they are more likely to reach a given number of years of covered employment by age 62 than are higher-educated workers. That belief is false; the SSA data show the opposite—earnings are positively correlated with years of Social Security–covered earnings at age 62 (Waldron 2012, Tables 4 and 5). Note that because the wage reflects returns-to-work experience, variable labor force attachment because of health or labor demand problems is unlikely to be conducive to high earnings levels. Favreault and Steuerle (2008) found similar results with education levels; those with higher education levels generally had more years of Social Security–covered work than those with lower education levels.
27 As Kingson and Brown (2009, 4) discuss, because of the automatic actuarial reduction for early retirement, "an EEA fixed at age 62 makes it more difficult to increase the FRA, since such increases would further erode the value of benefits for persons accepting them at age 62." For that reason, proposals to increase the FRA frequently include proposals to increase the EEA in tandem. As the authors note, "Thus, absent raising the EEA, it becomes increasingly difficult to justify an increase in the FRA, given the desire to maintain adequacy goals of Social Security" (23). Conversely, one less often sees policy proposals to increase the EEA without increasing the FRA. The reason for this is that the reduction in the projected OASDI actuarial shortfall comes from the increase in the FRA, not the increase in the EEA. An increase in the FRA is roughly equivalent to an across-the-board benefit cut in its impact on Social Security retired-worker benefits.
28 For entitlement to spouse and survivor benefits, the term couple can include divorced workers who had a marriage that lasted at least 10 years.
29 As reported in Myers (1993, Appendix 3-2), the original 1935 Social Security Act only included retirement benefits and was gender neutral, but the 1939 Act, which expanded the Social Security program to include benefits for auxiliaries (for example, spouses, survivors, and children), was not. Gender neutrality in the retired-worker program ended with the 1956 Act, in which the minimum retirement age was lowered to 62 for women but remained at 65 for men. The 1956 Act also changed the benefit formula for women to reflect the new lower age. In 1961, the age was lowered to 62 for men as well, but their benefit formula was calculated based on age 65 until the 1972 Act, which changed the male benefit formula to match the more generous female benefit formula beginning in 1975.
30 Relief in this case refers to the authors' suggestion that some workers still be allowed to claim at ages 62 and 63. As already noted, without holding the benefit reduction for the age-62 claim to 80 percent of the FRA, however, that policy option would not actually prevent the reduction in the monthly benefit amount for a worker claiming before the FRA. Zhivan and others (2008, 6) state, "the purpose of raising the EEA is to assure retirees a more adequate guaranteed monthly income." "Assure," in this context, implies that workers above a certain AIME level are made better off if they are no longer allowed to choose to claim at age 62 with a reduced benefit. In utility terms, such a position assumes workers are currently behaving irrationally or are not currently maximizing their utility.
31 Note that under the policy option suggested by Zhivan and others (2008) that would have held the benefit reduction for an age-62 claim to 80 percent of the FRA (as opposed to the 70 percent of the FRA scheduled under current law), this type of scenario would have represented a benefit increase for a higher-income individual relative to a lower-income individual.
32 This section uses the inclusive sample for analysis.
33 In the case of a couple, measured poverty would be lower, all other things equal, because household economies of scale are factored into the federal poverty line. In other words, the federal poverty line for a two-person family is not double the poverty line for a one-person family (SSA 2011, Table 3.E8).
34 The age difference between the persons in the married couple would also matter. For example, if a husband claimed at age 62 and his wife was 2 years younger, she would have had to wait 2 years to claim her own retired-worker benefit and her spouse benefit.
35 For comparison, refer to Waldron (2012, Charts 6 and 7) to see that eliminating both the foreign born and workers with mostly non-OASDI taxable earnings eliminates the presence of men with AIMEs at or below the current-law first bend point who have earnings from ages 45–55 in deciles 3 through 9.
36 The first of these 1972 groups, federal workers, will eventually disappear from the groups not covered by Social Security because all federal government workers newly hired after 1983 are covered.
37 For example, Schobel and McKay (1982) found that many workers eligible for the regular minimum were dually entitled, so that a decrease in the regular minimum would have been offset by an increase in the spouse benefit. In such a case, a regular minimum benefit would not have been costly, but only because the level of the benefit may have been set so low that full-time, year-round workers (for example, retired-worker primary-only beneficiaries) would have been unlikely to qualify.
38 For example, in 2010, the median income for family households was $61,544. By type of family, the median income of married couples was $72,751; of female householders, $32,031; and of male householders, $49,718 (DeNavas-Walt and others 2011, Table A-1). Also by type of family, 6.2 percent of married couples, 31.6 percent of female householders, and 15.8 percent of male householders were below poverty in 2010 (DeNavas-Walt and others 2011, Table 4).
39 Most proposals to increase the EEA are combined with proposals to increase the FRA. An increase in the FRA is a benefit reduction.
References
Aaron, Henry J., and Robert D. Reischauer. 2001. Countdown to Reform: The Great Social Security Debate. New York, NY: Century Foundation Press.
Adler, Nancy E., and Judith Stewart. 2010. "Health Disparities Across the Lifespan: Meaning, Methods, and Mechanisms." In Annals of the New York Academy of Sciences, Vol. 1186, 5–23.
Advisory Council on Social Security. 1997. Report of the 1994–1996 Advisory Council on Social Security, Volume 1: Findings and Recommendations. Washington, DC: 1994–1996 Advisory Council on Social Security. http://www.socialsecurity.gov/history/reports/adcouncil/report/toc.htm.
Allison, Paul D. 1995. Survival Analysis Using the SAS System: A Practical Guide. Cary, NC: SAS Institute.
Antonovsky, Aaron. 1967. "Social Class, Life Expectancy, and Overall Mortality." Milbank Memorial Fund Quarterly 45(2): 31–73.
Biggs, Andrew G. 2010. "The Case for Raising Social Security's Early Retirement Age." Retirement Policy Outlook, No. 3. Washington, DC: American Enterprise Institute for Public Policy Research (October). http://www.aei.org/article/economics/retirement/the-case-for-raising-social-securitys-early-retirement-age/.
[Board of Trustees] Board of Trustees of the Federal Old-Age and Survivors Insurance and Federal Disability Insurance Trust Funds. 2010. The 2010 Annual Report of the Board of Trustees of the Federal Old-Age and Survivors Insurance and Federal Disability Insurance Trust Funds. Washington, DC: Government Printing Office. http://www.socialsecurity.gov/oact/TR/2010/index.html.
Breeze, Elizabeth, Astrid E. Fletcher, David A. Leon, Michael G. Marmot, Robert J. Clarke, and Martin J. Shipley. 2001. "Do Socioeconomic Disadvantages Persist Into Old Age? Self-Reported Morbidity in a 29-Year Follow-Up of the Whitehall Study." American Journal of Public Health 91(2): 277–283.
Burkhauser, Richard V. 1996. "Touching the Third Rail: Time to Return the Retirement Age for Early Social Security Benefits to 65." Gerontologist 36(6): 726–727.
Burtless, Gary. 1998. "Increasing the Eligibility Age for Social Security Pensions." Testimony for the Special Committee on Aging, United States Senate (July 15). http://www.brookings.edu/research/testimony/1998/07/15saving-burtless.
Caldwell, Steven, and Theodore Diamond. 1979. "Income Differentials in Mortality: Preliminary Results Based on IRS-SSA Linked Data." In Statistical Uses of Administrative Records with Emphasis on Mortality and Disability Research, edited by Linda Del Bene and Fritz Scheuren, 51–59. Department of Health, Education, and Welfare, Social Security Administration, Office of Research and Statistics, Washington DC: Government Printing Office.
Committee for a Responsible Federal Budget. 2010. "Let's Get Specific: Social Security." Let's Get Specific Paper Series (September). http://crfb.org/sites/default/files/Lets_Get_Specific_Social_Security.pdf.
Cristia, Julian P. 2007. "The Empirical Relationship Between Earnings and Mortality." Working Paper Series. Washington DC: Congressional Budget Office (August).
Denavas-Walt, Carmen, Bernadette D. Proctor, and Jessica C. Smith. 2011. Income, Poverty, and Health Insurance Coverage in the United States: 2009. Census Bureau, Current Population Reports, P60-239. Washington DC: Government Printing Office.
Department of Health and Human Services. 1999 (estimate). Healthy People 2010: Understanding and Improving Health. http://www.healthypeople.gov/2010/Document/pdf/uih/uih.pdf.
Duggan, James E., Robert Gillingham, and John S. Greenlees. 2007. "Mortality and Lifetime Income: Evidence from U.S. Social Security Records." IMF Working Paper WP/07/15 (January). Washington, DC: International Monetary Fund, Fiscal Affairs Department.
Duleep, Harriet Orcutt. 1986. "Measuring the Effect of Income on Adult Mortality Using Longitudinal Administrative Record Data." Journal of Human Resources 21(2): 238–251.
———. 1989. "Measuring Socioeconomic Mortality Differentials Over Time." Demography 26(2): 345–351.
Duleep, Harriet Orcutt, and Daniel J. Dowhan. 2008. "Research on Immigrant Earnings." Social Security Bulletin 68(1): 31–50.
Goss, Stephen C. 2010. "The Future Financial Status of the Social Security Program." Social Security Bulletin 70(3): 111–125.
Gustman, Alan L., and Thomas L. Steinmeier. 2001. "How Effective is Redistribution Under the Social Security Benefit Formula?" Journal of Public Economics 82(1): 1–28.
Gustman, Alan L., Thomas L. Steinmeier, and Nahid Tabatabai. 2011. "The Effects of Changes in Women's Labor Market Attachment on Redistribution Under the Social Security Benefit Formula." NBER Working Paper No. 17439. Cambridge, MA: National Bureau of Economic Research (September).
Idler, Ellen L., and Yael Benyamini. 1997. "Self-Rated Health and Mortality: A Review of Twenty-Seven Community Studies." Journal of Health and Social Behavior 38(1): 21–37.
Johnson, Richard W. 2011. "Raise the Retirement Age, but Protect Those Who Can't Work." Urban Institute Spotlight on Poverty and Opportunity (February 28). http://www.urban.org/publications/901411.html.
Kingson, Eric R., and Yvonne Arsenault. 2000. "The Diversity of Risk Among Age-62 Retired Worker Beneficiaries." CRR Working Paper No. 2000-08. Chestnut Hill, MA: Center for Retirement Research at Boston College (November).
Kingson, Eric R., and Maria T. Brown. 2009. Are Age-62/63 Retired Worker Beneficiaries at Risk? CRR Working Paper No. 2009-13. Chestnut Hill, MA: Center for Retirement Research at Boston College (April).
Kitagawa, Evelyn M., and Philip M. Hauser. 1973. Differential Mortality in the United States: A Study in Socio-Economic Epidemiology. Cambridge, MA: Harvard University Press.
Krantz-Kent, Rachel. 2009. "Measuring Time Spent in Unpaid Household Work: Results from the American Time Use Survey." Monthly Labor Review 132(7): 46–59.
Kreider, Rose M., and Renee Ellis. 2011. Number, Timing, and Duration of Marriages and Divorces: 2009. Census Bureau, Household Economic Studies, Current Population Reports, P70-125. Washington, DC: Government Printing Office (May).
Marmot, Michael. The Status Syndrome: How Social Standing Affects Our Health and Longevity. 2004. New York, NY: Time Books, Henry Holt and Company, LLC.
Marmot, Michael, and Eric Brunner. 2005. "Cohort Profile: The Whitehall II Study." International Journal of Epidemiology 34(2): 251–256.
Marmot, Michael G., Martin J. Shipley, and Geoffrey Rose. 1984. "Inequalities in Death—Specific Explanations of a General Pattern?" The Lancet 323(8384): 1003–1006. As cited in Adler, Nancy E., and Judith Stewart. 2010. "Health Disparities Across the Lifespan: Meaning, Methods, and Mechanisms." Annals of the New York Academy of Sciences. Vol. 1186, 5–23.
Monk, Courtney, John A. Turner, and Natalia A. Zhivan. 2010. "Adjusting Social Security for Increasing Life Expectancy: Effects on Progressivity." CRR Working Paper No. 2010-9. Chestnut Hill, MA: Center for Retirement Research at Boston College (August).
Munnell, Alicia H. 2008. "Changing Employment Incentives and Claiming Behavior." Prepared for Policies to Facilitate Employment for Older Americans. Social Security Advisory Board (January). http://www.ssab.gov/documents/Paper-1MunnellSSABForum1-18-08.pdf.
Myers, Robert J. 1993. Social Security, 4th ed. Philadelphia, PA: Pension Research Council and University of Pennsylvania Press.
National Center for Health Statistics. 1998. Health, United States, 1998: With Socioeconomic Status and Health Chartbook. Hyattsville, MD.
———. 2012. Health, United States, 2011: With Special Feature on Socioeconomic Status and Health. Hyattsville, MD.
National Commission on Fiscal Responsibility and Reform. 2010. The Moment of Truth: Report of the National Commission on Fiscal Responsibility and Reform. http://www.fiscalcommission.gov/sites/fiscalcommission.gov/files/documents/TheMomentofTruth12_1_2010.pdf.
National Commission on Retirement Policy. 1999. The 21st Century Retirement Security Plan: Final Report of the National Commission on Retirement Policy. Washington, DC: Center for Strategic and International Studies, 38 (March).
Olsen, Kelly A., and Don Hoffmeyer. 2001/2002. "Social Security's Special Minimum Benefit." Social Security Bulletin 64(2): 1–15.
Pattison, David, and Hilary Waldron. 2008. "Trends in Elective Deferrals of Earnings from 1990–2001 in Social Security Administrative Data." Research and Statistics Note No. 2008-03 (June). http://www.socialsecurity.gov/policy/docs/rsnotes/rsn2008-03.html.
Pew Research Center. 2007. From 1997 to 2007: Fewer Mothers Prefer Full-Time Work. A Social & Demographic Trends Report. http://www.pewresearch.org/assets/social/pdf/WomenWorking.pdf.
Project on the Federal Social Role. 1985. The Report to the President of the Committee on Economic Security. In The Report of the Committee on Economic Security of 1935: And Other Basic Documents Relating to the Development of the Social Security Act—With Essays by Wilbur Cohen and Robert Ball, Chapter 2, 15–72. Washington DC: National Conference on Social Welfare. http://www.socialsecurity.gov/history/reports/ces.html.
Rendall, Michael S., Margaret M. Weden, Melissa M. Favreault, and Hilary Waldron. 2011. "The Protective Effect of Marriage for Survival: A Review and Update." Demography 48(2): 481–506.
Rosen, Shirwin, and Paul Taubman. 1979. "Changes in the Impact of Education and Income and Mortality in the U.S." In Statistical Uses of Administrative Records with Emphasis on Mortality and Disability Research, edited by Linda Del Bene and Fritz Scheuren, 61–66. Department of Health, Education, and Welfare, Social Security Administration, Office of Research and Statistics. Washington DC: Government Printing Office.
Schobel, Bruce D., and Steven F. McKay. 1982. "Characteristics of Newly Awarded Recipients of the Social Security Regular Minimum Benefit." Social Security Bulletin 45(6): 11–19.
Shkolnikov, Vladimir R., Rembrandt Scholz, Dmitiri A. Jdanov, Michael Stegmann, Hans-Martin von Gaudecker. 2008. "Length of Life and the Pensions of Five Million Retired German Men." European Journal of Public Health 18(3): 264–269.
Shoven, John B. 2007. "New Age Thinking: Alternative Ways of Measuring Age, Their Relationship to Labor Force Participation, Government Policies, and GDP." NBER Working Paper No. 13476. Cambridge, MA: National Bureau of Economic Research (October).
Smith, Creston M. 1989. "The Social Security Administration's Continuous Work History Sample." Social Security Bulletin 52(10): 20–28.
Smith, Ralph. 1999. Raising the Earliest Eligibility Age for Social Security Benefits. Washington, DC: Congressional Budget Office.
Social Security Administration. 2011. Annual Statistical Supplement to the Social Security Bulletin, 2010. Washington, DC: Office of Retirement and Disability Policy, Office of Research, Evaluation, and Statistics.
Springstead, Glenn R. 2011. "Distributional Effects of Accelerating and Extending the Increase in the Full Retirement Age." Policy Brief No. 2011-01. Social Security Administration, Office of Retirement Policy, Office of Policy Analysis (January). http://www.socialsecurity.gov/policy/docs/policybriefs/pb2011-01.html.
SSA. See Social Security Administration.
Stapleton, David C. 2009. Employment Support for the Transition to Retirement: Can a New Program Help Older Workers Continue to Work and Protect Those Who Cannot? Washington, DC: AARP Public Policy Institute (April).
Steuerle, C. Eugene. 2011. "Restoring Solvency and Improving Equity in Social Security: Benefit Options." Statement before the Subcommittee on Social Security, Committee on Ways and Means, United States House of Representatives (July 8). http://www.urban.org/UploadedPDF/901435-Improving-Equity-in-Social-Security.pdf.
van Rossum, Caroline T. M., Martin J. Shipley, Hendrike van de Mheen, Diederick E. Grobbee, Michael G. Marmot. 2000. "Employment Grade Differences in Cause Specific Mortality: A 25 Year Follow Up of Civil Servants from the First Whitehall Study." Journal of Epidemiological Community Health 54(3): 178–184.
Waldron, Hilary. 2001. "Links Between Early Retirement and Mortality." ORES Working Paper Series No. 93. Washington, DC: Social Security Administration, Office of Policy, Office of Research, Evaluation, and Statistics (August). http://www.socialsecurity.gov/policy/docs/workingpapers/wp93.pdf.
———. 2004. "Heterogeneity in Health and Mortality Risk Among Early Retiree Men." ORES Working Paper Series No. 105. Washington, DC: Social Security Administration, Office of Policy, Office of Research, Evaluation, and Statistics (May). http://www.socialsecurity.gov/policy/docs/workingpapers/wp105.html.
———. 2007. "Trends in Mortality Differentials and Life Expectancy for Male Social Security–Covered Workers, by Socioeconomic Status." Social Security Bulletin 67(3): 1–28. http://www.socialsecurity.gov/policy/docs/ssb/v67n3/v67n3p1.html.
———. 2012. "The Sensitivity of Proposed Social Security Benefit Formula Changes to Lifetime Earnings Definitions." Social Security Bulletin 72(2): 1–22. http://www.socialsecurity.gov/policy/docs/ssb/v72n2/v72n2p1.html.
———. Forthcoming. "A Review of Research on the Distributional Effects of Raising Social Security's Early Entitlement Age."
Wolfson, Michael, Geoff Rowe, Jane F. Gentleman, and Monica Tomiak. 1993. "Career Earnings and Death: A Longitudinal Analysis of Older Canadian Men." Journal of Gerontology 48(4): S167–S179.
Zhivan, Natalia, Seven A. Sass, Margarita Sapozhnikov, and Kelly Haverstick. 2008. "An 'Elastic' Earliest Eligibility Age for Social Security." Issue in Brief No. 8-2. Chestnut Hill, MA: Center for Retirement Research at Boston College (February). http://crr.bc.edu/wp-content/uploads/2008/02/IB_8-2.pdf.