The Effects of Alternative Demographic and Economic Assumptions on MINT Simulations: A Sensitivity Analysis
Research and Statistics Note No. 2014-03 (released April 2014)
Patrick Purcell is with the Office of Research, Evaluation, and Statistics, Office of Retirement and Disability Policy (ORDP), Social Security Administration (SSA). Dave Shoffner is with the Office of Retirement Policy, ORDP, SSA.
Acknowledgments: For helpful comments during the review process, the authors thank Paul Davies, Howard Iams, Joni Lavery, and Mark Sarney. The authors also thank Melissa Favreault, Owen Haaga, and Karen Smith for technical assistance with the MINT simulations.
The findings and conclusions presented in this note are those of the authors and do not necessarily represent the views of the Social Security Administration.
Introduction to MINT
| MINT | Modeling Income in the Near Term |
| OCACT | Office of the Chief Actuary |
| SIPP | Survey of Income and Program Participation |
| SSA | Social Security Administration |
In the late 1990s, the Social Security Administration's (SSA's) Office of Research, Evaluation, and Statistics initiated development of a microsimulation model1 to estimate the retirement income of the baby boom generation—the 78 million Americans who were born between 1946 and 1964. SSA developed the resulting model, named Modeling Income in the Near Term (MINT), with assistance from the Brookings Institution, the RAND Corporation, and the Urban Institute.
MINT can estimate the individual and family incomes of future retirees and simulate the distributional effects of policy proposals, taking into account the diverse socioeconomic and demographic traits of the US population. To develop these estimates, MINT requires detailed information about workers' past earnings, their marital and fertility histories, and other characteristics such as race, education, and disability status. In addition, MINT simulations require as inputs projections of future real interest rates, wage growth, and trends in mortality and disability.
MINT uses Social Security earnings records as its source information about workers' past earnings. The Census Bureau's Survey of Income and Program Participation (SIPP) is MINT's main source of data on the size and demographic traits of the US population.2 SSA's Office of the Chief Actuary (OCACT) provides estimates of future interest rates, inflation rates, wage growth rates, and population mortality and disability rates, along with other economic and demographic assumptions.
Historically, MINT simulations have been based on OCACT's intermediate-cost projections of future interest rates, inflation rates, wage growth, and mortality and disability rates. Estimates of future rates of return on stocks held in retirement accounts typically have been drawn from a distribution with the same mean and standard deviation as historical rates of return. In this note, we present the results of MINT simulations based on alternative projections of future rates of mortality and disability and projected rates of return on stocks that differ from the historical mean. We compare the results to simulations based on OCACT's intermediate-cost projections. Our research objective is to test the sensitivity of MINT simulations to changes in specific inputs to the model and to document the results of the alternative simulations.
The simulation results described in this note were produced using version six of MINT (MINT6).3 MINT6 matches the survey records of participants in the 2001 and 2004 panels of the SIPP to their Social Security earnings records through 2009.4 The model uses the projections of future interest rates, inflation rates, wage growth, and trends in rates of mortality and disability that were developed by OCACT for The 2011 Annual Report of the Board of Trustees of the Federal Old-Age and Survivors Insurance and Federal Disability Insurance Trust Funds (hereafter, referred to as the “Trustees Report”).5 MINT6 includes only participants in the 2001 and 2004 panels of the SIPP who were born between 1926 and 1975. All of these individuals were at least 34 years old in 2009, the base year for our simulations, and all will be at least 65 years old in 2040, the year for which we present our simulation results.
Assumptions in the Trustees Report
OCACT annually prepares estimates for the Board of Trustees of the revenues and expenditures of the Social Security trust funds over the next 75 years. The actuaries prepare those estimates using three sets of economic and demographic assumptions, referred to as the “low-cost,” “intermediate-cost,” and “high-cost” scenarios.6 The Trustees Report describes the intermediate-cost assumptions as reflecting the Trustees' best estimate of future experience. However, the report also presents estimates based on low-cost and high-cost alternative demographic and economic assumptions “to show a wide range of possible outcomes, because assumptions related to these factors are subject to uncertainty” (Board of Trustees 2011, 34).
The low-cost and high-cost projections represent scenarios that would be, respectively, particularly favorable or unfavorable to the long-run financial status of the trust funds. The Trustees Report states that future costs are “unlikely to be as extreme as either of the outcomes portrayed by the low- and high-cost projections” (ibid., 15). Nevertheless, each of the individual economic and demographic assumptions in those scenarios falls within a range that the actuaries have deemed to be plausible. Thus, the low-cost and high-cost estimates for specific variables represent reasonable alternatives for testing the sensitivity of MINT simulations to changes in the economic and demographic variables on which the model's projections are based.
SSA uses OCACT's intermediate-cost economic and demographic assumptions exclusively in MINT simulations of proposed changes to Social Security taxes, benefits, and eligibility. However, because economic and demographic projections are uncertain, simulations based on alternative assumptions can inform policymakers about other possible outcomes. MINT simulations based on alternative demographic assumptions also can help those who use the model understand which variables have the greatest impact on its projections. The results of simulations based on alternative assumptions also might reveal aspects of the model that could benefit from refinement or revision.
Simulating Alternative Assumptions in MINT
The Trustees' low-cost and high-cost demographic and economic projections differ from the intermediate-cost projections in several ways. The low-cost alternative includes a higher total fertility rate, a slower decline in the mortality rate, a higher real-wage differential, a higher real interest rate, and a lower unemployment rate. The high-cost alternative includes a lower total fertility rate, a more rapid decline in the mortality rate, a lower real-wage differential, a lower real interest rate, and a higher unemployment rate. In our first two simulations, we used OCACT's low-cost and high-cost rates of mortality and disability in place of the intermediate-cost projections. In our third and fourth simulations, we changed the real rate of return on equities held in retirement accounts from a projection centered on the historical mean—first to a higher and then to a lower mean annual real rate of return. In each simulation, we changed only one of those parameters so that the effects of each change would be apparent in the simulation results.
In the first of our four alternative simulations, we replaced the intermediate-cost mortality and disability rates with the low-cost (higher mortality, lower disability) projections. In the second simulation, we used the high-cost (lower mortality, higher disability) projections. We examined the effects of the alternative mortality and disability estimates on the projected size and composition of the population aged 65 or older in 2040.
In our third and fourth alternative simulations, we used a mean annual real rate of return for stocks held in retirement accounts that differed from the baseline rate of return. In the baseline simulation, the projected mean annual real rate of return on common stocks was drawn from a distribution with a mean and standard deviation equal to the mean annual real rate of return on large-company stocks from 1951 through 2010. Over that period, the mean annual real rate of return on large-company common stocks was 6.5 percent, with a standard deviation of 17.4 percent. In our third simulation, we increased the future mean annual real rate of return by 2 percentage points to 8.5 percent. In the fourth simulation, we reduced the future mean annual real rate of return by 2 percentage points to 4.5 percent. In both cases, real rates of return were assumed to vary according to the historical standard deviation. Later in the note, we describe the impact of the alternative rates of return on stocks on the retirement account balances of persons aged 65 or older in 2040.
Mortality in the MINT Baseline Simulation
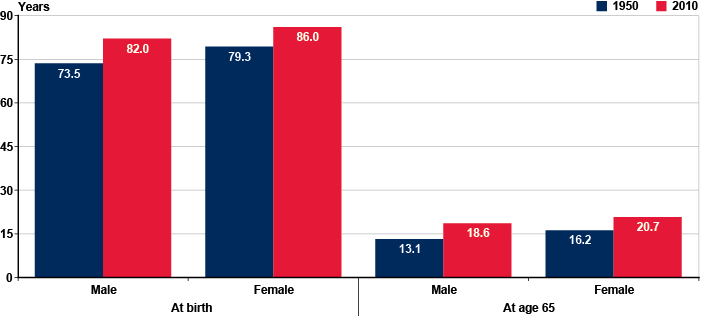
Life expectancy at birth and at older ages has been increasing in the United States for many years. For example, Chart 1 shows that in 1950, male life expectancy at birth was 73.5 years, and female life expectancy at birth was 79.3 years. Life expectancy for men at age 65 was 13.1 years in 1950, and for women at age 65 it was 16.2 years. In 2010, estimated male life expectancy at birth was 82.0 years, and female life expectancy at birth was 86.0 years. Life expectancy for men at age 65 was 18.6 years in 2010, and for women at age 65 it was 20.7 years. Those gains in life expectancy have not been uniformly distributed across the population. In general, improvements in life expectancy have been smaller for blacks, persons with less education, and those with lower lifetime earnings than for whites, persons with college degrees, and those who have above-average lifetime earnings (Waldron 2002, 2007, 2013; Denney and others 2010; Masters, Hummer, and Powers 2012).
Life expectancy for males and females at birth and at age 65, 1950 and 2010
| Year | At birth | At age 65 | ||
|---|---|---|---|---|
| Male | Female | Male | Female | |
| 1950 | 73.5 | 79.3 | 13.1 | 16.2 |
| 2010 | 82.0 | 86.0 | 18.6 | 20.7 |
OCACT projects that life expectancy will continue to increase over the 75-year projection period. However, mortality rates in the low-cost, intermediate-cost, and high-cost projections differ in the rate at which future mortality rates are expected to decline. For example, under the intermediate-cost projections, life expectancy for men at age 65 will increase from 18.6 years in 2010 to 20.6 years by 2040. For women, life expectancy at age 65 is projected to increase from 20.7 years in 2010 to 22.6 years by 2040. By contrast, under the low-cost (high mortality) assumptions, life expectancy for men at age 65 will rise from 18.0 years in 2010 to 18.8 years by 2040, and for women at age 65 it will rise from 20.1 years to 20.8 years in the same period. Under the high-cost (low mortality) assumptions, life expectancy for men at age 65 will rise from 19.4 years in 2010 to 23.0 years by 2040, and for women at age 65 it will rise from 21.6 years to 24.9 years in the same period.7
The Trustees Report cautions readers that the low-cost and high-cost projections “are not intended to suggest that all parameters would be likely to differ from the intermediate values in the same direction, but are intended to illustrate the effect of clearly defined scenarios that are, on balance, very favorable or unfavorable for the program's financial status” (Board of Trustees 2011, 15). For example, the low-cost scenario combines higher mortality rates with lower disability rates than those projected in the intermediate scenario. Likewise, the high-cost scenario combines lower mortality rates and higher disability rates than those projected in the intermediate-cost scenario. This does not preclude the possibility that higher mortality rates might occur along with higher disability rates or that lower rates of mortality might occur in conjunction with lower rates of disability.8
Simulation Results: Effects of Higher or Lower Rates of Mortality
MINT models mortality in two ways, depending on an individual's age. Before age 65, the probability that an individual will die between age X and age X+5 is modeled by matching that person's record to the record of a “donor”—a similar person who has already aged from age X to age X+5. If the donor died during that 5-year interval, the person with whom that record was matched also died in his or her imputed-age interval. From age 65 onward, MINT uses a hazard model to project mortality. The hazard model incorporates differential mortality for respondents based on disability, marital status, sex, education, and lifetime income. In both methods, the mortality estimates derived from the “match” model and the hazard model are aligned with the Trustees' mortality projections.
OCACT projects mortality rates by age, sex, and cause of death (Board of Trustees 2011, 79). Consequently, MINT simulations based on the low-cost and high-cost mortality and disability projections change both the estimated number of older people in future years and the estimated distribution of the population by age, sex, and marital status. The distribution of the population by marital status is affected mainly because different mortality rates would change the proportion of elderly people who are married or widowed. In our simulations of the population aged 65 or older in 2040, the alternative mortality projections resulted in greater changes in the distribution of the population by age, sex, and marital status than by race and education.
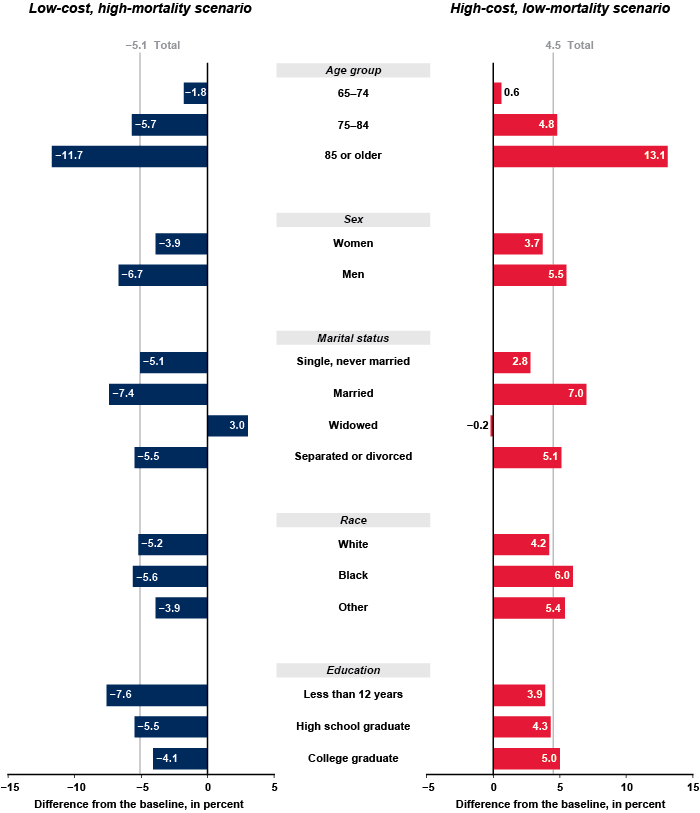
For the projected population aged 65 or older in 2040, Chart 2 compares the baseline simulation with both the low-cost, high-mortality scenario and the high-cost, low-mortality scenario.9 The figures show the percentage change in the population under each alternative compared with the baseline scenario. Under the low-cost, high-mortality scenario, the total number of persons aged 65 or older in 2040 would be 5.1 percent lower than it would be under the baseline scenario.10 However, the number of persons aged 65 to 74 would be just 1.8 percent lower than it would be under the baseline scenario, and the number of persons aged 85 or older would be almost 12 percent lower. There would be 6.7 percent fewer men, but just 3.9 percent fewer women. The change in the age and sex composition of the population would affect the distribution of the aged population by marital status. Under the high-mortality projections, the number of married individuals aged 65 or older would be 7.4 percent lower than in the baseline case, while the number of widow(er)s would be 3.0 percent higher. There would be 7.6 percent fewer persons aged 65 or older with less than a high school education compared with the overall decline in the elderly population of 5.1 percent. The decrease in the population among older blacks would be slightly larger than that for whites and people of other races.11
Under the high-cost, low-mortality scenario shown in Chart 2, the population aged 65 or older would be 4.5 percent larger in 2040 compared with the baseline projection. The number of persons aged 65 to 74 would increase by just 0.6 percent, but the number of persons aged 85 or older would be 13.1 percent higher than the baseline projection. The number of men would increase by 5.5 percent, and the number of women would increase by 3.7 percent. The number of aged individuals who are married would be 7.0 percent higher than under the baseline, intermediate-cost scenario. The number of widow(er)s would be essentially unchanged. The number of blacks would rise by 6.0 percent under the low-mortality assumptions, but the distribution of the aged population by education would not change much compared with the distribution in the baseline simulation.
Average Social Security Benefits Under Alternative Mortality Assumptions
Mortality rates that differ from the baseline scenario would affect the number of people aged 65 or older in future years and the distribution of the aged population by age, sex, and marital status. Total annual Social Security benefit payments obviously would change in the same direction as the change in the total aged population; however, mean and median Social Security benefits for each beneficiary category would change relatively little. This is mainly because the difference in mortality rates in the three alternative scenarios is greatest at older ages—after the working lives of the persons on which Social Security benefits are based. Table 1 shows mean and median Social Security income in 2040 for all beneficiaries aged 65 or older by type of benefit. Expressed as a percentage of the national average wage, neither mean nor median Social Security benefits would differ greatly under any of the three different mortality scenarios.12
| Type of benefit | Intermediate cost (baseline) | Low cost (high mortality) | High cost (low mortality) | |||
|---|---|---|---|---|---|---|
| Mean | Median | Mean | Median | Mean | Median | |
| Retired worker | ||||||
| Social Security income | 31.7 | 30.6 | 31.8 | 30.7 | 31.5 | 30.5 |
| Total family income | 276.7 | 137.3 | 276.7 | 136.0 | 287.3 | 139.3 |
| Spouse | ||||||
| Social Security income | 17.9 | 18.0 | 17.9 | 18.0 | 17.7 | 17.9 |
| Total family income | 391.7 | 159.8 | 397.1 | 157.2 | 412.7 | 160.7 |
| Widow(er) | ||||||
| Social Security income | 31.7 | 31.1 | 32.1 | 31.7 | 31.5 | 31.1 |
| Total family income | 188.4 | 80.3 | 189.6 | 82.5 | 196.6 | 78.2 |
| Disabled worker | ||||||
| Social Security income | 30.1 | 28.1 | 30.7 | 28.9 | 31.3 | 30.3 |
| Total family income | 105.5 | 68.6 | 118.9 | 71.2 | 143.2 | 78.5 |
| SOURCE: Authors' calculations using Modeling Income in the Near Term, Version 6. | ||||||
| NOTE: Data are expressed as percentages of the national average wage in 2040. | ||||||
Rates of Return to Retirement Accounts in the MINT Baseline Simulation
MINT simulates the accumulation of retirement wealth in employer-sponsored defined contribution plans and individual retirement accounts (IRAs). Baseline estimates of retirement account ownership, contributions, and account balances are derived from SIPP data, which are then aligned to data from the Survey of Consumer Finances (SCF).13 MINT's baseline simulation projects that there will be 72.6 million persons aged 65 or older in 2040, and that 75.2 percent of those individuals will own one or more retirement accounts.14 MINT allocates contributions to retirement accounts between stocks and bonds based on data from the SCF. Contributions are allocated according to a multinomial logit that takes into account the individual's age, education, marital status, and risk tolerance.15 Each individual is assigned one of five allocations between stocks and bonds: (1) 0 percent in stocks; (2) 20 percent in stocks; (3) 50 percent in stocks, (4) 80 percent in stocks; or (5) 100 percent in stocks.
To bring account balances up to the baseline year of the simulation, MINT applies the actual mean annual rates of return to account balances from the last year for which a balance was reported in the SIPP through 2010. From 2011 through 2017, a real annual rate of return of 7.4 percent is applied. Beginning with 2018, every account is assigned an annual rate of return drawn from a distribution with the mean and standard deviation of historical real rates of return since 1951.16 Over that period, the mean annual real rate of return on large company stocks was 6.5 percent, with a standard deviation of 17.4 percent.17
In our alternative simulations, we examined the effect on retirement account balances in 2040 of mean real rates of return on stocks 2 percentage points higher and 2 percentage points lower than the historical mean rate of return of 6.5 percent. In all simulations, the standard deviation on stock market returns was 17.4 percent. To isolate the effects of alternative rates of return on stocks on retirement wealth, bond returns were unchanged from the baseline.18
The effects of alternative mean rates of return on stocks on retirement account assets in MINT simulations depend in part on the number of years to which the alternative rates of return are applied. In 2040, the members of the 1975 birth cohort—the youngest cohort in MINT6—will be 65 years old. The stochastic simulations of rates of return begin in 2018, when people born in 1975 will turn age 43. Thus, even for the youngest birth cohort members in the model, the simulated returns apply to a maximum of 22 years before they reach age 65. For older birth cohort members, the simulated returns apply to even fewer years before they reach age 65. If the simulations applied alternative rates of return to a greater number of years before retirement age, they would yield larger differences from the baseline simulation. Another factor influencing the effect of alternative stock market rates of return is the proportion of retirement account assets invested in stocks. In the 1998 through 2007 SCFs, 56 percent of retirement account balances were invested in stocks (Smith and others 2010, Table 5-7, V-15). As people approach retirement, they allocate more of their retirement account assets to bonds, which is reflected in MINT. If more retirement assets were invested in stocks, the effect of altering the rate of return on stocks would be greater.
Effect on Retirement Account Balances of Alternative Rates of Return on Equities
Charts 3 and 4 illustrate the effects on account balances in 2040 of rates of return on stocks that differ from those in the baseline simulation. Both charts are restricted to persons who own one or more retirement accounts. Chart 3 examines all persons aged 65 or older in 2040. Chart 4 focuses on persons aged 65 to 69 in 2040, the members of the 1971 through 1975 birth cohorts. That younger subpopulation will spend a greater proportion of the simulation period in their preretirement years accumulating retirement assets than those who were born earlier.
Retirement account balances in 2040 among all persons aged 65 or older, relative to the national average wage
| Account balance percentile | Account balance as a mulitple of national average wage | Percentage change from baseline | |||
|---|---|---|---|---|---|
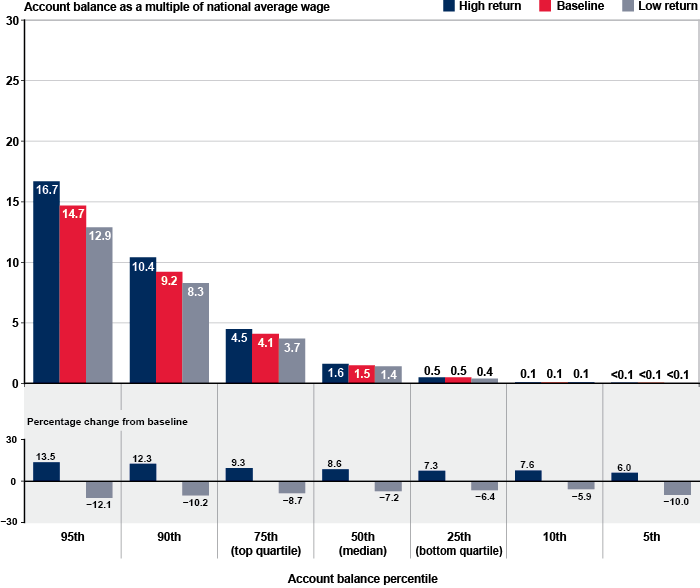
| High return | Baseline | Low return | High return | Low return | |
| 95th | 16.7 | 14.7 | 12.9 | 13.5 | -12.1 |
| 90th | 10.4 | 9.2 | 8.3 | 12.3 | -10.2 |
| 75th (top quartile) | 4.5 | 4.1 | 3.7 | 9.3 | -8.7 |
| 50th (median) | 1.6 | 1.5 | 1.4 | 8.6 | -7.2 |
| 25th (bottom quartile) | 0.5 | 0.5 | 0.4 | 7.3 | -6.4 |
| 10th | 0.1 | 0.1 | 0.1 | 7.6 | -5.9 |
| 5th | <0.1 | <0.1 | <0.1 | 6.0 | -10.0 |
Retirement account balances in 2040 among persons aged 65 to 69, relative to the national average wage
| Account balance percentile | Account balance as a mulitple of national average wage | Percentage change from baseline | |||
|---|---|---|---|---|---|
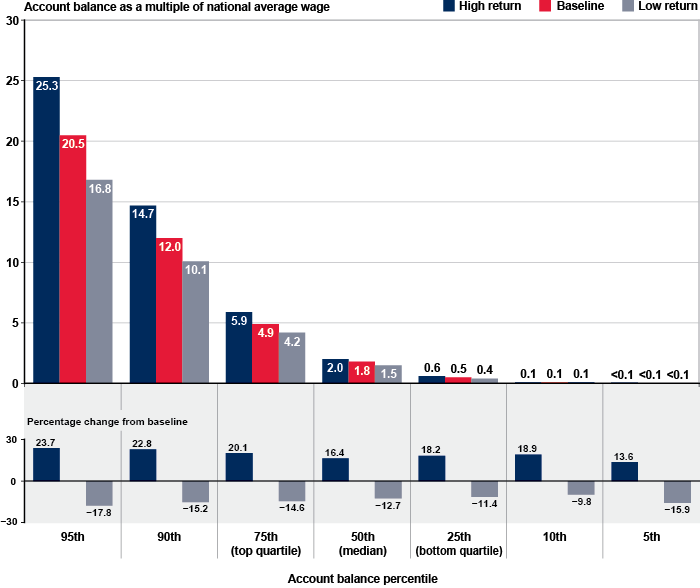
| High return | Baseline | Low return | High return | Low return | |
| 95th | 25.3 | 20.5 | 16.8 | 23.7 | -17.8 |
| 90th | 14.7 | 12.0 | 10.1 | 22.8 | -15.2 |
| 75th (top quartile) | 5.9 | 4.9 | 4.2 | 20.1 | -14.6 |
| 50th (median) | 2.0 | 1.8 | 1.5 | 16.4 | -12.7 |
| 25th (bottom quartile) | 0.6 | 0.5 | 0.4 | 18.2 | -11.4 |
| 10th | 0.1 | 0.1 | 0.1 | 18.9 | -9.8 |
| 5th | <0.1 | <0.1 | <0.1 | 13.6 | -15.9 |
Under the baseline simulation, the median retirement account balance in 2040 among all persons aged 65 or older is estimated to be equal to 1.5 times the national average wage (Chart 3).19 One-fourth of account owners in that age group have estimated balances equal to 4.1 times the national average wage or more, and another fourth have estimated account balances equal to half the national average wage or less. Under the high rate-of-return simulation, the median account balance would be equal to 1.6 times the national average wage, and under the low rate-of-return scenario, the median retirement account balance would be 1.4 times that national average wage. Relative to the baseline scenario, the median account balance would be 8.6 percent higher under the high rate-of-return scenario and 7.2 percent lower under the low rate-of-return scenario.
Under each rate-of-return scenario, the median account balance among persons aged 65 to 69 in 2040 is estimated to be slightly larger than the median account balance among all persons aged 65 or older (Chart 4). The main reasons for this result are (1) the greater number of simulation years that those individuals would have spent in preretirement compared with all persons aged 65 or older, and (2) the fewer number of years in retirement that most of them would have had to spend money from their accounts. Among persons aged 65 to 69 in 2040, the median account balance under the baseline scenario would be 1.8 times the national average wage. Under the high and low rate-of-return scenarios, the median account balances for this group would be 2.0 times and 1.5 times the national average wage, respectively.
Relative to the baseline, the percentage difference in account balances under the high-return and low-return scenarios also would be larger among persons aged 65 to 69 in 2040 than it would be among all persons aged 65 or older. Under the high rate-of-return scenario, the median account balance among persons aged 65 to 69 in 2040 would be 16.4 percent higher than it would be in the baseline case. Under the low rate-of-return scenario, the median account balance among persons in the same age group in 2040 would be 12.7 percent lower than it would be in the baseline simulation.
Discussion and Conclusion
MINT can estimate the income of future retirees under current law, and it can simulate changes in the amount and distribution of retirement income under a wide range of policy proposals. Historically, MINT simulations have been based exclusively on the demographic and economic projections produced by OCACT under its intermediate-cost scenario. The alternative projections developed under the high-cost and low-cost scenarios can be used to test the sensitivity of MINT simulations to changes in specific inputs to the model. Because projections are inherently uncertain, the alternative projections also can provide policymakers with estimates of the income of the retired population in future years if economic or demographic trends diverge from the intermediate-cost path.
We estimated the size and demographic characteristics of the population aged 65 or older using OCACT's high-cost and low-cost projections of future rates of mortality and disability. We found that under both projections, the size of the aged population in 2040 would differ by about 5 percent from the baseline projection, and the distribution of the aged population by age, sex, and marital status also would change. Mean and median Social Security benefits would change relatively little compared with the baseline simulation.
We also simulated the effect on retirement account balances of adjusting the future mean annual rate of return on stocks 2 percentage points higher and 2 percentage points lower than the historical real mean rate of return of 6.5 percent. We found that if the mean annual real rate of return on stocks held in retirement accounts were adjusted 2 percentage points higher than the historical mean, retirement account balances in 2040 would be almost 9 percent greater than they would be under the baseline scenario. A mean annual real rate of return adjusted 2 percentage points lower than the historical average would reduce the median account balance in 2040 by about 7 percent. The effects on retirement account balances would be greater for individuals aged 65 to 69 in 2040 than they would be for those aged 70 or older in the same year.
OCACT's low-cost and high-cost projections of rates of mortality and disability incorporate assumptions that are particularly favorable or unfavorable to the long-run balance of the Social Security trust funds. The low-cost scenario combines higher rates of mortality and lower rates of disability than the intermediate-cost projections. The high-cost scenario combines lower rates of mortality and higher rates of disability than the intermediate-cost projections. Under the low-cost scenario, when the projections of higher mortality rates and lower disability rates are combined in MINT, the effect of the higher mortality rates on the size of the future aged population is partly offset by the lower disability rates. This occurs because one of the determinants of the annual hazard of mortality after age 65 is whether the individual was ever disabled. Likewise, under the high-cost scenario, the lower rates of mortality are partly offset by the effect that the higher rates of disability have on the hazard model's estimates of mortality after age 65.
Further sensitivity analysis of the MINT model might include simulations in which only the mortality rates are changed to the high-cost and low-cost rates, while disability rates are maintained at the same levels as in the intermediate-cost scenario. Another useful sensitivity test would be to run simulations in which real wages grow faster or more slowly than they would under the intermediate-cost scenario. Rates of wage growth that differ from the intermediate-cost projections would affect mean and median benefit amounts, and thus could possibly have a substantial impact on the economic security of future retirees. An alternative sensitivity test that might provide useful information to policymakers would be to simulate future rates of wage growth that differ for workers with different levels of education. Some studies have found that in recent years, wages have tended to grow faster for workers with earnings in the top half of the earnings distribution than for workers with earnings in the lower half. Career-average earnings are positively correlated with education. To the extent that less-educated workers continue to experience below-average rates of wage growth, their income in retirement could fall below the amounts that are implied by the average annual rate of real wage growth projected in the intermediate-cost scenario.
Appendix
| Characteristic | Intermediate cost (baseline) | Low cost (high mortality) | High cost (low mortality) | |||
|---|---|---|---|---|---|---|
| Number (thousands) | Percent | Difference (thousands) | Percentage difference | Difference (thousands) | Percentage difference | |
| Total | 72,573 | 100.0 | -3,730 | -5.1 | 3,260 | 4.5 |
| Age group | ||||||
| 65–74 | 31,604 | 43.6 | -584 | -1.8 | 178 | 0.6 |
| 75–84 | 27,542 | 38.0 | -1,574 | -5.7 | 1,324 | 4.8 |
| 85 or older | 13,427 | 18.4 | -1,572 | -11.7 | 1,758 | 13.1 |
| Sex | ||||||
| Women | 39,687 | 54.7 | -1,542 | -3.9 | 1,466 | 3.7 |
| Men | 32,886 | 45.3 | -2,189 | -6.7 | 1,793 | 5.5 |
| Marital status | ||||||
| Single, never married | 5,682 | 7.9 | -290 | -5.1 | 157 | 2.8 |
| Married | 38,348 | 53.0 | -2,842 | -7.4 | 2,677 | 7.0 |
| Widowed | 14,289 | 19.8 | 425 | 3.0 | -32.0 | -0.2 |
| Separated or divorced | 14,002 | 19.4 | -772 | -5.5 | 710 | 5.1 |
| Race | ||||||
| White | 60,571 | 83.5 | -3,138 | -5.2 | 2,567 | 4.2 |
| Black | 7,530 | 10.4 | -420 | -5.6 | 452 | 6.0 |
| Other | 4,473 | 6.2 | -173 | -3.9 | 241 | 5.4 |
| Education | ||||||
| Less than 12 years | 5,215 | 7.2 | -397 | -7.6 | 203 | 3.9 |
| High school graduate | 42,398 | 58.4 | -2,311 | -5.5 | 1,818 | 4.3 |
| College graduate | 24,960 | 34.4 | -1,023 | -4.1 | 1,239 | 5.0 |
| Type of Social Security benefit | ||||||
| Retired worker | 52,244 | 72.0 | -3,076 | -5.9 | 2,815 | 5.4 |
| Spouse | 5,617 | 7.7 | -501 | -8.9 | 393 | 7.0 |
| Widow(er) | 11,704 | 16.1 | 54 | 0.5 | -106 | -0.9 |
| Disabled worker | 698 | 1.0 | -31 | -4.4 | 80 | 11.5 |
| Not a beneficiary | 2,311 | 3.2 | -176 | -7.6 | 77 | 3.3 |
| SOURCE: Authors' calculations using Modeling Income in the Near Term, Version 6. | ||||||
| NOTE: Totals do not necessarily equal the sum of rounded components. | ||||||
Notes
1 A microsimulation model is a computer program that uses information about a representative sample of “micro units”—such as individuals, families, or households—to estimate how changes in their characteristics or behavior will affect the entire population or a subset of that population, such as workers or retirees.
2 The SIPP represents the civilian, noninstitutionalized resident population of the 50 states and the District of Columbia. It does not include residents of nursing homes or prisons, military personnel living on base, or residents of US territories. The Social Security area population includes the SIPP population plus those other groups. The Social Security area population is about 3.0 percent to 3.5 percent larger than the population represented by SIPP. Further information about the SIPP can be found at http://www.census.gov/sipp/.
3 SSA is currently developing MINT7, which uses data from the 2004 and 2008 panels of the SIPP.
4 For the 2001 panel of the SIPP, 67 percent of individuals' survey records were matched to their Social Security earnings records. For the 2004 panel of the SIPP, the match rate was 88 percent. Earnings were imputed for nonmatched records (Smith and others 2010, Table 1-1, I-2.)
5 The full 2011 Trustees Report is available at http://www.socialsecurity.gov/oact/tr/2011/tr2011.pdf.
6 The low-cost, intermediate-cost, and high-cost scenarios are also referred to as alternative I, alternative II, and alternative III, respectively. The low-cost scenario assumes higher mortality rates and lower disability rates than those in the baseline, intermediate-cost scenario. The high-cost scenario assumes lower mortality rates and higher disability rates than those in the baseline, intermediate-cost scenario. We examine the effects of the alternative mortality and disability rates on the size and composition of the population aged 65 or older in 2040. Disability Insurance beneficiaries are converted to old-age beneficiary status when they reach the full retirement age (FRA). Persons aged 65 to 66 in 2040 will be below their FRA of 67. Persons aged 67 or older will have reached their FRA.
7 Higher rates of mortality would be less costly than the baseline projections, and higher rates of disability would be more costly. Higher mortality rates imply fewer beneficiaries at a given point in time, and vice versa.
8 In the future, we plan to run a MINT simulation that combines the higher mortality rates from the low-cost scenario with the higher disability rates from the high-cost scenario. Then we will combine the lower disability rates from the low-cost scenario with the lower mortality rates from the high-cost scenario.
9 For the numbers of persons on which Chart 2 is based, see the Appendix table.
10 OCACT estimates that under the intermediate-cost mortality assumptions, there would be 79.7 million persons aged 65 or older in the Social Security area in 2040. Under the low-cost, high-mortality assumptions, there would be 76.0 million persons aged 65 or older, or 4.6 percent fewer than under the intermediate-cost assumptions. Under the high-cost, low-mortality assumptions, there would be 84.0 million persons aged 65 or older, or 5.4 percent more than under the intermediate-cost assumptions (Board of Trustees 2011, Table V.A2, 88–89).
11 The “Other” category comprises mainly Asian Americans, but also includes people of Native American heritage.
12 In Table 1, benefits are standardized as a percentage of the national average wage to allow comparison across time, taking into account the effects of inflation and real wage growth. Discounted for inflation, the national average wage in 2040 is estimated to be approximately $60,750 under the intermediate-cost scenario.
13 For more information, see Smith and others (2010, chap. 5).
14 This includes both employer-sponsored accounts, such as 401(k) plans and IRAs. In some cases, the individual's spouse owns the account. A spouse's account is treated here as a joint resource.
15 Variation in risk tolerance among individuals is imputed from variables on the 1998 through 2007 SCFs. The SCF asks respondents about their willingness to accept greater investment risk in exchange for the possibility of earning higher investment returns. Willingness to accept investment risk generally declines with age.
16 Owners of retirement accounts are assumed to pay administrative fees equal to 1 percent of assets per year, which reduces the net rate of return on the accounts.
17 For ease of exposition, we changed only the mean annual rate of return on stocks. For other purposes, one might vary the rates of return on both stocks and bonds, taking into account relevant covariances.
18 In MINT, rates of return on bonds and stocks are each drawn from distributions based on their historical means and standard deviations. The draws of stock rates of return are independent of the draws of bond rates of return. Future model development may incorporate the covariance of these rates of return for each annual return drawn.
19 The account balance represents the sum of all of the individual's retirement accounts.
References
[Board of Trustees] Board of Trustees of the Federal Old-Age and Survivors Insurance and Disability Insurance Trust Funds. 2011. The 2011 Annual Report of the Board of Trustees of the Federal Old-Age and Survivors Insurance and Federal Disability Insurance Trust Funds. Washington, DC: Government Printing Office. http://www.socialsecurity.gov/oact/tr/2011/tr2011.pdf.
Denney, Justin T., Richard G. Rogers, Robert A. Hummer, and Fred C. Pampel. 2010. “Education Inequality in Mortality: The Age and Gender Specific Mediating Effects of Cigarette Smoking.” Social Science Research 39(4): 662–673.
Masters, Ryan K., Robert A. Hummer, Daniel A. Powers. 2012. “Educational Differences in U.S. Adult Mortality: A Cohort Perspective.” American Sociological Review 77(4): 548–572.
Smith, Karen E., Melissa M. Favreault, Barbara A. Butrica, and Philip Issa. 2010. Final Report: Modeling Income in the Near Term Version 6. Washington, DC: Urban Institute (December). http://www.urban.org/UploadedPDF/412479-Modeling-Income-in-the-Near-Term-Version-6.pdf.
Waldron, Hilary. 2002. “Mortality Differentials by Race.” ORES Working Paper Series No. 99. Washington, DC: Office of Research, Evaluation, and Statistics, Social Security Administration.
———. 2007. “Trends in Mortality Differentials and Life Expectancy for Male Social Security–Covered Workers, by Average Relative Earnings.” ORES Working Paper Series No. 108. Washington, DC: Office of Research, Evaluation, and Statistics, Social Security Administration.
———. 2013. “Mortality Differentials by Lifetime Earnings Decile: Implications for Evaluations of Proposed Social Security Law Changes.” Social Security Bulletin 73(1): 1–37.