Incorporating Immigrant Flows into Microsimulation Models
Social Security Bulletin, Vol. 68, No. 1, 2008 (released August 2008)
Complementing the second paper's focus on forecasting immigrant earnings and emigration in a "closed system" for a given population, the last article of the trilogy explores how to project immigrant earnings for an "open system"—a system that includes future immigrants. A simple method to project future immigrants and their earnings is presented.
The authors are with the Division of Economic Research, Office of Research, Evaluation, and Statistics, Office of Retirement and Disability Policy, Social Security Administration; Duleep is also a Research Professor with the Thomas Jefferson Program in Public Policy, College of William and Mary and a Research Fellow with IZA, Institute for the Study of Labor.
Contents of this publication are not copyrighted; any items may be reprinted, but citation of the Social Security Bulletin as the source is requested. The findings and conclusions presented in the Bulletin are those of the authors and do not necessarily represent the views of the Social Security Administration.
Summary
Building on the research on immigrant earnings reviewed in the first article of this series, "Research on Immigrant Earnings," the preceding article, "Adding Immigrants to Microsimulation Models," linked research results to various issues essential for incorporating immigrant earnings into microsimulation models. The discussions of that article were in terms of a closed system. That is, it examined a system in which immigrant earnings and emigration are forecast for a given population represented in the base sample in the microsimulation model. This article, the last in the series, addresses immigrant earnings projections for open systems—microsimulation models that include projections of future immigration. The article suggests a simple method to project future immigrants and their earnings. Including the future flow of immigrants in microsimulation models can dramatically affect the projected Social Security benefits of some groups.
Introduction
The preceding article, (Duleep and Dowhan 2008a), focused on forecasting immigrant earnings and emigration for a given population represented in the base sample of the microsimulation model. For many purposes, microsimulation models form a closed system, predicting for an existing population. Some issues, however, demand that the model permit new entrants into the system: people marry, babies come into the world, and new immigrants arrive.
Social Security's Modeling Income in the Near Term (MINT) model, for instance, originally projected for a population represented by data from the 1990–1993 Survey of Income and Program Participation (SIPP) and ignored any post-1993 population growth fueled by immigration. To assess the future well-being of the elderly, Social Security analysts decided that MINT needed to forecast the earnings and retirement income of future U.S. elderly populations, including immigrants who entered the United States after the SIPP surveys of MINT's base sample. Moreover, if microsimulation were to supplement the actuarial forecasts of Social Security's financial status, future immigration would need to be projected.
Incorporating new immigrants into a microsimulation model poses two challenges—the flow of immigrants into the country needs to be projected and the new entrants' earnings profiles imputed. These pursuits are closely related since the characteristics that modelers include in the immigrant projections define what can be done in the immigrant earnings projections.
Projecting the Flow of Immigrants
In the sections that follow, two approaches for projecting immigrant flows are discussed: a time-series approach, where recent trends are used to forecast future trends, and a structural approach involving three steps: (1) determining the variables that affect immigration, (2) estimating the relationships between the predictor variables and immigration, and (3) projecting the predictor variables and their corresponding estimated immigration effects into the future. Combining elements of the time series and structural approaches, a new approach for projecting immigrant flows is introduced.
Using Recent Trends to Forecast Future Trends
U.S. immigration policy, the political state of the world, and various characteristics of the United States and other countries' economies affect the flow of immigrants to the United States. All of those factors are difficult (perhaps impossible) to project. Lacking a crystal ball to forecast their future fate, a pragmatic alternative is to use recent trends in U.S. immigration to forecast future trends. Recent immigration conveys a great deal of information about future immigration because once individuals begin to migrate to the United States from a particular region of the world, U.S. networks and paths are established and the process tends to continue.1
Although once established, migration patterns tend to persist, changes in immigration policy as well as changing circumstances in both the United States and in immigrant source countries occur and can affect both the magnitude and composition of immigration. For this reason, data that are continuously updated are needed to quickly capture changes in immigrant flows and incorporate them into the projections. At the same time, transitory influences, such as backlogs in the administration of immigrant visas, occur for a variety of reasons and may affect immigration for a particular year with no long-term implications. To parse out the persistent from the transitory requires data that can be averaged over several years. Annual data that is continuously updated would allow tracking changes in trends as well as averaging over several years.
Projections of the number of immigrants, by year of immigration, should also be done by characteristics that are associated with distinct immigrant earnings patterns. This way, projections of immigrants' earnings can be linked to the projected immigration. As discussed in the first article of this series, Duleep and Dowhan (2008b), human capital (often measured by age and years of schooling) affects the earnings of immigrants and U.S. natives. However, for immigrants, the degree to which their country-of-origin human capital transfers to the U.S. labor market also affects their earnings.
If the human capital that immigrants possess transfers easily to the U.S. labor market, immigrant earnings profiles resemble those of similarly educated and experienced U.S. natives. The less home-country skills transfer to the U.S. labor market, the lower the initial earnings of immigrants (relative to otherwise similar U.S. natives), but the higher their earnings growth, a phenomenon that likely reflects a higher propensity to invest in U.S. human capital. A key predictor of immigrant skill transferability is the source country's level of economic development. These arguments suggest that the ideal data for projecting immigration would classify immigrants by source country; the source country data could in turn be linked to annually updated data on the economic development of countries of the world.2
Some policy issues are relevant to legally admitted immigrants. Others relate to undocumented immigrants, still others relate to all immigrants. The ideal data source should permit separating the legal from the illegal immigrant population. Modelers could then tailor simulations to their own particular needs. Currently, little is known about illegal immigrants.
The aforementioned requirements—continuously updated historical records of U.S. immigration by legal status and country of origin—recommend using the annual records of the Office of Immigration Statistics (OIS) of the Department of Homeland Security (formerly known as the Immigration and Naturalization Service) as the primary data source for projecting future trends in immigration. These records contain the numbers and characteristics (age and gender) of all newly admitted legal immigrants by country of origin for each year.
Alternative data collected annually, such as the American Community Survey (ACS) files or the Current Population Survey (CPS) all contain, to an unknown degree, undocumented immigrants. In contrast, the OIS information, by its very nature, pertains solely to the legal population.3 Modelers can separately add information on the undocumented in accordance with the latest research on undocumented immigrants available at the time of the projections.
The OIS annual data allow modelers to track trends and to average over several years. A straightforward approach for projecting future immigration would be to average immigration over recent years, dividing by source-region categories that are relevant to projecting immigrant earnings. Since the OIS data represent all immigrant source countries, modelers face no constraints in tailoring OIS-based projections to the source-country grouping used in their particular immigrant earnings projection model.
In using recent trends to project future trends, it is important to bear in mind significant policy changes that may have temporary effects. For instance, the Immigrant Reform and Control Act (IRCA) of 1986, provided for the legalization of 3.0 million residential undocumented immigrants.4 In choosing past years to average and project future years, modelers might want to pick years beyond IRCA's initial effect. Recent research by Beach, Green, and Worswick (2008) shows an association between the host country's economic conditions and the numbers and age composition of immigrants. In years with exceptionally good economic conditions, a greater percent of immigrants are young. Their research suggests that to project future immigration, modelers may want to exclude from the averaging period years of exceptionally good or exceptionally poor economic conditions.5
Barring changes that temporarily increase or decrease immigration, averages over the most recent 5 years for which data are available might be used to forecast the near future. The fact that the OIS data are easily accessible and continuously updated means that the straightforward immigrant projection system described here could be easily updated, ad infinitum. As OIS data are updated, the multiyear averaging period would be similarly updated. To facilitate linking immigration projections to earnings projections, the immigration by source-country projections should be linked to data on economic development indicators.6
The easiest way to proceed is to use the OIS published tables associated with the statistical yearbook. These tables are available on the internet and provide, in one place, yearly trends in the number of immigrants by country of origin.
A shortcoming of these easy-to-use tabulations is that they do not have the age distributions of immigrants for all source countries or regions. One possibility would be to impose the overall age distribution of immigrants, which is available each year in the OIS published tables, on each source country/region used in the projections. This approach would be acceptable if immigrant age distributions across countries of origin were similar, or at least uncorrelated with source-country factors that affect earnings profiles, in particular, the economic development level of the source country.
To gauge the importance of intercountry variations in immigrant age distributions we used public-use microsample data from the 1980 and 1990 censuses to estimate the age distribution of immigrants, divided by country of origin (Chart 1).7 In general, young adults are more heavily represented in economically developing countries versus economically developed countries.
Distribution of immigrants by age at time of entry and source-country category (economically developing versus developed countries), based on the 1980 and 1990 Census PUMS (percent)
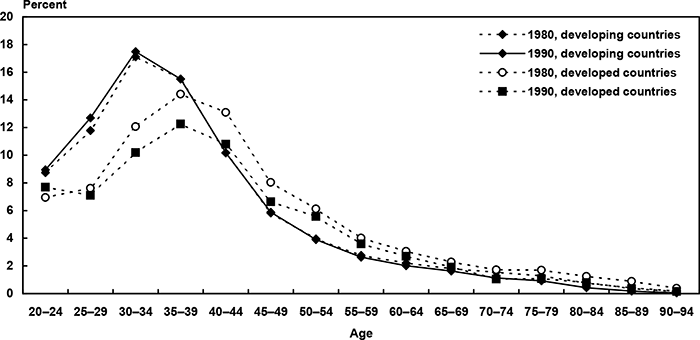
| Age | Developing countries | Developed countries | ||
|---|---|---|---|---|
| 1980 | 1990 | 1980 | 1990 | |
| 20–24 | 8.7 | 8.9 | 6.9 | 7.7 |
| 25–29 | 11.8 | 12.7 | 7.6 | 7.1 |
| 30–34 | 17.1 | 17.5 | 12.1 | 10.2 |
| 35–39 | 15.5 | 15.5 | 14.4 | 12.3 |
| 40–44 | 10.2 | 10.2 | 13.1 | 10.8 |
| 45–49 | 5.8 | 5.9 | 8.0 | 6.6 |
| 50–54 | 4.0 | 3.9 | 6.1 | 5.6 |
| 55–59 | 2.8 | 2.6 | 4.0 | 3.6 |
| 60–64 | 2.2 | 2.0 | 3.1 | 2.7 |
| 65–69 | 1.8 | 1.6 | 2.3 | 1.9 |
| 70–74 | 1.5 | 1.1 | 1.7 | 1.1 |
| 75–79 | 1.3 | 0.9 | 1.7 | 1.1 |
| 80–84 | 0.8 | 0.4 | 1.2 | 0.8 |
| 85–89 | 0.4 | 0.2 | 0.9 | 0.4 |
| 90–94 | 0.2 | 0.1 | 0.4 | 0.2 |
The OIS provides access to individual records of legal immigrant admissions through public-use tapes that are available annually. From these data records, the age/gender distribution for each source country/region could be calculated. The analysis of immigrant age distributions by source country suggests that for the proposed immigration projection system, a system should be established to inform Social Security immigrant projections with OIS data on individuals.
Another issue with using the OIS records as the primary data source for projecting future immigration trends is that the records lack information on the education of immigrants. Yet, as with age, immigrant education distributions vary by country of origin (Funkhouser and Trejo 1995).8
Remedying the education deficit requires supplementing the OIS data with survey data.9 The sample sizes for immigrants in several annual surveys with education information, such as the CPS, are small. Due solely to sampling variability, large year-to-year variations in the immigrant education levels by source country occur in these surveys. One possible strategy for overcoming the sample size constraint would be to use information on incoming immigrants averaged over several consecutive surveys. Another possibility would be to rely on decennial census data to fill in the missing information in the OIS-based projections. A shortcoming of the decennial census data, however, is their infrequency. The best option, in terms of both sample size and frequency, is the recently instituted annual American Community Survey (ACS) data. Whatever the data source, the modeler would want to proceed by using the survey data to measure education for the country-of-origin/gender/age groups detailed by the OIS data since the distribution of immigrant education by source country varies with the age and gender of immigrants.10
Beacons of Immigration Change
The projection methodology thus far is a time series approach—current and past immigration predicts future immigration. Another approach for projecting immigration is a structural one. Variables that affect immigration are determined through research. Having determined the relevant variable set, the relationship between these predictors of immigration and immigration is estimated. The predictors of immigration are then projected into the future, along with the corresponding estimated immigration responses.
The difficulty with the structural approach lies not with estimating the relationship between the predictor variables and immigration, which can be done using historical and cross-sectional data, but with the inherent difficulty of projecting the future path of the predictor variables. The limitation of the time-series approach is that the view of the future is limited to what the present and recent past encapsulate.
A middle-ground strategy would be to combine elements of both the time-series and structural approaches. Specifically, assume that recent immigration generally predicts future immigration, but supplement the time-series predicted paths with "beacons of change." This could be done by using annual data to track key predictors of immigration. When a clear change in one of the predictor variables becomes apparent, the time-series based immigration projections would change according to the estimated "structural" relationships between the predictor variables and immigration.
The key variables to track would be those that research, conducted over many time periods and across countries, has shown to have a clear effect on immigration. One such variable is immigration policy. Given that a policy change is expected to be lasting, the country-specific immigration trajectories would change according to the estimated effect of the policy change on immigration.
The age composition of each source country is another key variable to track. Theoretically, the younger migrants are, the longer the payoff time from migration; opportunity costs also increase with age—as one works in a particular locality and firm, it becomes increasingly difficult to transfer the accumulated work experience. Empirically, a large body of research shows that most adult immigrants are young.11 A country's age distribution thus determines the population of potential immigrants. When a significant change in a country's age distribution is detected, the projected trajectory of that country's U.S. immigration would be altered to reflect this change.12
A third key variable is a country's level of economic development. Substantial research documents the following characteristics of the relationship between economic development and migration.13
- At the very lowest levels of economic development, people do not migrate—it is not the poorest of the poor who migrate.
- When a certain economic threshold is passed, migration from poor to rich regions begins. Once started, the migration persists, fueled by the networks and paths established by earlier migrants.
- Migration decreases as the source-country/destination-country differential in economic development narrows.
As discussed in the preceding article (Duleep and Dowhan 2008a), source-country economic development also affects immigrant emigration from the United States.
In this proposed projection system, the economic development of all countries, relative to the United States would be tracked. In supplementing the times-series projection approach, the most important countries to track would be those that are currently big contributors to U.S. immigration as well as those countries that are not big contributors, but potentially could be. For countries that are currently big U.S. immigration contributors, the relevant question is whether the situation will change. A large upswing in their economic development relative to the United States would signify such a change in both their immigration and U.S. emigration trajectories. For countries that are potential contributors, passing a certain economic-development threshold could signify the beginning of an important flow of immigration.
In determining when a clear change in one of the predictor variables has occurred, modelers would need to set up a system to identify persistent stable changes in one direction. For instance, a positive increase in a country's gross national product (GNP) over a 5-year period might be a satisfactory indicator of a persistent stable change.
To use this proposed projection system requires predicting changes in immigration trajectories as a function of changes in the tracked predictor variables. One approach would be to use estimates (based on cross-sectional and time-series data) of the relationship between changes in policy, economic development, age structure, and changes in immigration. Another approach would be to mimic the MINT methodology approach (described in Duleep and Dowhan 2008a), wherein the earnings trajectories of older persons are used to project the earnings trajectories of younger persons. In like fashion, the experiences of similar countries—that went through a similar transition in the recent past—could serve as donors for a country's projected immigration trajectory.
By utilizing the knowledge that is in the recent landscape of U.S. immigration by source country, the proposed projection approach acknowledges the inertia that is inherent to immigration flows. Yet it also permits updating those predictions in response to changes in three key variables (immigration policy, age structure, and economic development) that are easily tracked annually. A key assumption underlying this approach is that recent immigration is a good predictor of future immigration until there is a significant change in one of the key predictor variables. On the road to projecting immigration, this system might be called "The Past is Prologue" with acknowledged important bumps.
Giving the New Immigrants Earnings Profiles
Armed with trends in the number of immigrants by earnings relevant characteristics, the microsimulation modeler is now poised to bring these projected immigrants to life by giving them earnings profiles. As discussed in the preceding article (Duleep and Dowhan 2008a), there are three general methods used to forecast individual earnings in microsimulation models: the "human capital" approach, the "past-is-prologue" approach, and the "donor" approach.
Without any earnings information, it is impossible to project earnings profiles for future immigrants with the past-is-prologue approach. Nor can earnings be projected with the method introduced in the preceding article (Duleep and Dowhan 2008a) that uses the distance between immigrants' initial earnings and the earnings of similarly experienced and educated natives to predict immigrant earnings growth.
It is possible to estimate earnings as a function of the projected characteristics, and simulate an earnings profile for each age-gender-education-country of origin combination. However, as discussed in the preceding article, a possible limitation of a parametric approach is the limited variation in earnings profiles across the projected individuals.14 An alternative approach to project the earnings of future immigrants is to choose donors from the model's base population and clone their earnings profiles on the new immigrants.15
The lessons learned from research on immigrant earnings in the first article (Duleep and Dowhan 2008b), should inform the donor selection process. Since immigrants and U.S. natives have distinctly different earnings profiles, even controlling for age and education, immigrants, not natives, should serve as donors for the model's new immigrants. The profound change over time in immigrant earnings profiles suggests that donors be chosen from the subsample of immigrants in the base population who came to the United States after 1979. Important earnings profile differences across immigrants associated with the economic development of their home countries suggests that source-country divisions that capture these differences should be used to select donors. Finally, immigrant earnings profiles vary according to the age at which immigrants enter the United States. Sample size constraints may prohibit picking donors from a model's base population of post-1979 immigrants within detailed age-at-migration categories. In this case, a sensible approach would be to aggregate age-at-migration categories into three categories: migrated at young working ages (for example, ages 20–39); migrated at older working ages (for example, ages 40–59); and migrated at near retirement and retirement ages (for example, ages 60 or older).
In summary, to bring the projected immigrants to life, microsimulation modelers can pick donors by first stratifying the base sample of immigrants who immigrated after 1979 by gender, age at migration, and source region. Donors for the new immigrants can then be chosen in accordance with the projected numbers of future immigrants and their earnings cloned onto the new immigrants. Using the same stratification scheme, modelers can also choose emigrants from the population of new (donor-created) immigrants, in accordance with the emigration methodology used in the preceding article (Duleep and Dowhan 2008a).
The proposed projection methodology for incorporating future immigrant flows into microsimulation models reflects recent immigration trends and takes into account earnings pattern variations among immigrants and between immigrants and natives. It also takes into account immigrant emigration. Key among its advantages is that it can be easily updated on a continuous basis using readily available data.
Projecting Undocumented Immigrants
The discussion of projection methodology thus far has not explicitly treated illegal immigration. Although many data sources include illegal immigrants to an unknown degree, information on the undocumented per se is scarce. Much of it comes from nonstatistical studies. These studies strongly suggest that the undocumented differ from legal immigrants in terms of their age, source-country composition, and emigration. Yet it is difficult to derive from such approaches numbers to use for a model's projections.
A statistical approach called the "residual method" can be used to inform estimates of the undocumented immigrant population.16 Starting with the number of immigrants in a survey such as the Decennial Census or CPS, the residual method estimates immigrant population growth as if the only source of growth was the immigration of legal immigrants, as accurately counted by the OIS annual records. Taking into account the (estimated) extent to which the Census or CPS undercounts immigrants, the number of immigrants in a later survey minus the estimated legal immigration growth provides an estimate of the undocumented immigrant population. Based on the residual method, Passel (1999) estimated that about 520,000 illegal immigrants enter the United States each year.
The residual method also provides information on some of the likely characteristics of the undocumented immigrant population. The age distribution of the undocumented differs radically from that of the legal immigrant population: The undocumented are younger (Chart 2). They are also far more likely to come from Central America, particularly Mexico, than are legal immigrants (Chart 3). To capture these differences in a microsimulation model, the age and source-country distribution shown in Charts 2 and 3 could be imposed on the illegal immigrants estimated to enter the country each year.
Distribution of legal versus illegal immigrants, by age at time of entry (percent)
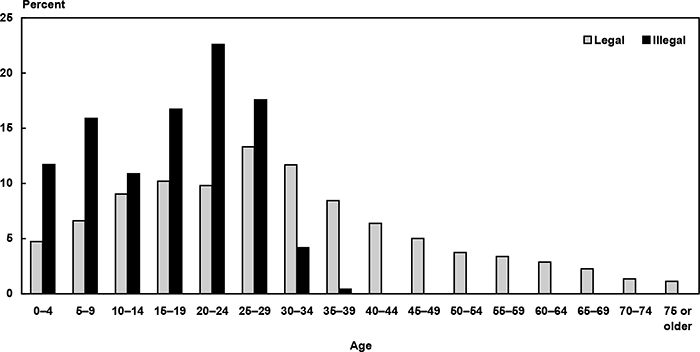
| Age | Legal | Illegal |
|---|---|---|
| 0–4 | 4.7 | 11.7 |
| 5–9 | 6.6 | 15.9 |
| 10–14 | 9.0 | 10.9 |
| 15–19 | 10.2 | 16.7 |
| 20–24 | 9.8 | 22.6 |
| 25–29 | 13.3 | 17.6 |
| 30–34 | 11.7 | 4.2 |
| 35–39 | 8.4 | 0.4 |
| 40–44 | 6.4 | . . . |
| 45–49 | 5.0 | . . . |
| 50–54 | 3.7 | . . . |
| 55–59 | 3.4 | . . . |
| 60–64 | 2.9 | . . . |
| 65–69 | 2.3 | . . . |
| 70–74 | 1.4 | . . . |
| 75+ | 1.1 | . . . |
| NOTE: . . . = not applicable. | ||
Distribution of legal versus illegal immigrants, by source country (percent)
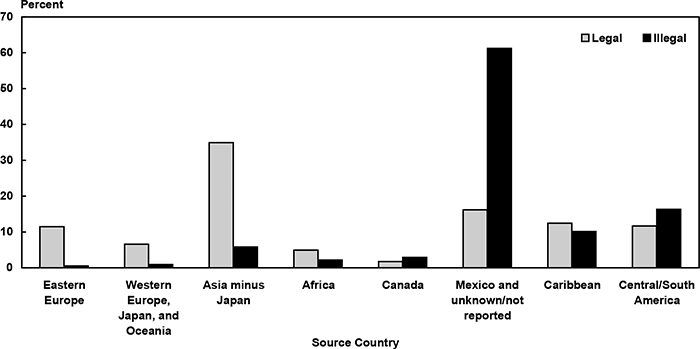
| Source country | Legal | Illegal |
|---|---|---|
| Eastern Europe | 11.5 | 0.5 |
| Western Europe, Japan, and Oceania | 6.6 | 0.9 |
| Asia minus Japan | 34.9 | 5.8 |
| Africa | 5.0 | 2.2 |
| Canada | 1.7 | 2.9 |
| Mexico and unknown/not reported | 16.2 | 61.2 |
| Caribbean | 12.5 | 10.1 |
| Central/South America | 11.7 | 16.3 |
A pragmatic approach for projecting future trends of the undocumented is to use recent past trends to forecast future trends. As with immigrants in general, the recent past is informative since once the undocumented begin to migrate to the United States from a particular region of the world, U.S. networks are established and the process tends to continue. Yet, unlike legal immigration, no administrative record source exists that explicitly counts the undocumented entering the United States each year.
A time series of annual "counts" of the undocumented, by region of origin and age, could be created and annually updated using the residual method with annual data such as the CPS or ACS. With such a continually updated time series of estimated counts, projections of future undocumented immigration based on recent average experience, could be made. With regard to "beacons of change," the key variables that affect legal immigration—source countries' level of economic development, their age structure, and U.S. immigration policy—also affect undocumented immigration and could be incorporated into the projection methodology.
Adding Future Immigrants Can Affect Policy Predictions
Including future flows of immigrants can dramatically affect policy predictions from microsimulation models. For instance, Social Security's MINT model simulates the economic welfare of the future aged population. Using some of the projection methods outlined in this article, immigration was incorporated into the MINT model. Doing so increased both the size of the projected population and its composition. With the closed MINT model, 10.7 percent of retirees in 2020 are projected to be foreign born. With the addition of new immigrants, the share of foreign-born retirees increased to 14.4 percent. The closed MINT system projected that 7.9 percent of the elderly population in 2020 would be Hispanic. That share increased to 9.3 percent with new immigrants added to the model.
Including future immigrant flows to the MINT model also affected the projected Social Security benefits of groups. Social Security benefits are typically computed using the average indexed monthly earnings (AIME). The average summarizes up to 35 years of a worker's earnings. From the AIME, the primary insurance amount (PIA) is computed. The PIA is the basis for benefits that are to be paid.
Adding new immigrants decreased the population mean AIME in 2020, from 78 percent to 75 percent of the economy-wide average wage. Though modest, the significance of this change increases when particular groups are considered. The mean AIME of Hispanics and Asians fell by 17 percent and 25 percent, respectively. Prior to the addition of new immigrants, only 4.3 percent of men born between 1961 and 1965 were projected to be ineligible for Social Security's Old-Age insurance. With their inclusion, this percentage increased to 10.3 percent. These examples underscore the potential importance of including future immigrants in microsimulation models.
Notes
1. Many scholars have documented the role persistence plays in migration patterns via family relationships, networks, and paths blazed by prior migrants. See, for instance, Bauer, Epstein, and Gang (2002), Boyd (1989), Epstein and Gang (2004), Gurak and Caces (1992), and Jasso and Rosenzweig (1986).
2. There are two potential sources of data that could be used for this purpose: the World Development Indicators database, published by the World Bank, which has more than 550 development indicators with time series for over 200 countries or country groups from 1960 to the present (World Bank 2005), and the Penn World Tables (Heston, Summer, and Aten 2002; Heston and Summers 1991).
3. The National Immigration Survey pertains solely to documented immigration, but is not available on an annual basis.
4. Beginning in 1987, those who had resided continuously in the United States since January 1982 could apply for permanent resident status under the amnesty provisions of IRCA. Under those provisions, 1.7 million applied for amnesty, and another 1.3 million applied as Specialized Agricultural Workers, a program that was much more lenient (only 90 days of continuous agricultural employment in the past year) in requirements for legalization.
5. An alternative approach would be to model the effect of economic conditions on immigration, or to use the estimates from Beach, Green, and Worswick (2008) to inform the projections. The problem with this approach is that it assumes that future economic conditions can be reasonably predicted.
6. Refer to note 2 for information on two potential sources of data that could be used for this purpose.
7. Chart 2 gives statistics for men and women combined; separate analyses by gender relate the same story.
8. By picking donors to represent new immigrants by country of origin (discussed in the next section), the educational distribution of immigrants will be represented. The adequacy of this approach will depend on the size of the base sample from which the donors are chosen. A disadvantage of this approach, regardless of the base sample's size, is that it does not allow updating the education distribution of immigrants by country of origin, but rather freezes it at what is represented in the models' base sample data.
9. Another approach, described in note 8, could also be pursued.
10. A problem with using ACS, CPS, or Census data to fill in the missing education information in the projections is that these data sources include to an unknown extent illegal aliens. Comparing the education information by source country from these sources with the information collected in the New Immigrant Survey (Jasso, Massey, Rosenzweig, and Smith 2000), a survey that follows one cohort of legal immigrants, would help gauge how the inclusion of illegal aliens affects the education results.
11. The age pattern of migration is well documented. See, for instance, U.S. Census Bureau (1996) and Fertig and Schmidt (2000).
12. Each country's age distribution could be tracked using the Census Bureau's International Data Base, a computerized data bank containing statistical tables of demographic data for 228 countries and areas around the world.
13. A few examples of research documenting this relationship include Hatton and Williamson (1992, 1994), Massey and Zenteno (1999), and Volger and Rotte (2000).
14. Variation in earnings profiles across the projected individuals will be limited to the demographic/human capital divisions used in the earnings regressions.
15. As discussed in Duleep and Dowhan 2008a, the donor approach to modeling earnings in microsimulation models will, by design, be the most successful in representing variation in immigrant earnings profiles because the donors that "donate" the projected earnings profile come from the existing population of immigrants and thereby represent the extant variation in earnings profiles within any demographic/human capital group.
16. Another approach, principally associated with the work of Bob Warren of the former Immigration and Naturalization Service, constructs estimates of the undocumented immigrant population by combining detailed statistics by year of entry for each component of change that contributes to the undocumented immigrant population residing in the United States. Refer to Warren (1994, 1998).
References
Bauer, Thomas, Gil S. Epstein, and Ira N. Gang. 2002. Herd effects of migration networks? The location choice of Mexican immigrants in the U.S. IZA Discussion Paper No. 551. Bonn: Institute for the Study of Labor.
Beach, Charles M., Alan G. Green, and Christopher Worswick. 2008. The impacts of the point system and immigrant class on skill characteristics of immigrant inflows: The experience of Canada. Paper presented at the Conference on Immigration: Trends, Consequences and Prospects for the United States.
Boyd, Monica 1989. Family and personal networks in international migration: Recent developments and new agendas. International Migration Review 23(3): 638–670.
Duleep, Harriet Orcutt, and Daniel J. Dowhan. 2008a. Adding immigrants to microsimulation models. Social Security Bulletin 68(1): 51–66.
———. 2008b. Research on immigrant earnings. Social Security Bulletin 68(1): 31–50.
Epstein, Gil S., and Ira N. Gang. 2004. The influence of others on migration plans. IZA Discussion Paper No. 1244. Bonn: Institute for the Study of Labor.
Fertig, Michael, and Christoph M. Schmidt. 2000. Aggregate-level migration studies as a tool for forecasting future migration streams. IZA Discussion Paper No. 183. Bonn: Institute for the Study of Labor.
Funkhouser, Edward, and Stephen J. Trejo. 1995. The labor market skills of recent male immigrants: Evidence from the Current Population Survey. Industrial and Labor Relations Review 48(4): 792–811.
Gurak, Douglas T., and Fe Caces. 1992. Migration networks and the shaping of migration systems. In International migration systems: A global approach, M. Kritz, L. Lim, and H. Zlotnik, eds., 150–176. Oxford: Oxford University Press.
Hatton, Timothy J., and Jeffrey G. Williamson. 1992. International development and world migration: A historical perspective. NBER Historical Paper No. 41. Cambridge, MA: National Bureau of Economic Research.
–––—. 1994. Migration and the international labor market, 1850–1939. London: Routledge.
Heston, Alan, and Robert Summers. 1991. The Penn World Table (Mark 5): An expanded set of international comparisons, 1950–1988. Quarterly Journal of Economics: 327–368.
Heston, Alan, Robert Summers, and Bettina Aten. 2002. Penn World Table Version 6.1. Philadelphia, PA: Center for International Comparisons, University of Pennsylvania. Available at http://pwt.econ.upenn.edu/.
Jasso, Guillermina, Douglas S. Massey, Mark R. Rosenzweig, and James P. Smith. 2000. The New Immigrant Survey Pilot (NIS-P): Overview and new findings about U.S. legal immigrants at admission. Demography 37(1): 127–136.
Jasso, Guillermina, and Mark R. Rosenzweig. 1986. Family reunification and the immigration multiplier: U.S. immigration law, origin-county conditions and the reproduction of immigrants. Demography 23(3): 291–311.
Massey, Douglas S., and Rene M. Zenteno. 1999. The dynamics of mass migration. Proceedings of the National Academy of Sciences 96(9): 5328–5335.
Passel, Jeffrey S. 1999. Undocumented immigration to the United States: Numbers, trends, and characteristics. In Illegal immigration in America, David W. Haines and Karen E. Rosenblum, eds., 27–111. CT: Greenwood Press.
U.S. Census Bureau. 1996. Population projections of the United States by age, sex, race and Hispanic origin: 1995–2050. Current Population Reports P25-114. Washington, DC: U.S. Census Bureau.
Vogler, Michael, and Ralph Rotte. 2000. The effects of development on migration: Theoretical issues and new empirical evidence. Journal of Population Economics 13(3): 485–508.
Warren, Robert. 1994. Estimates of the unauthorized immigrant population residing in the United States, by country of origin and state of residence: October 1992. Unpublished paper. U.S. Immigration and Naturalization Service.
———. 1998. Illegal alien resident population. Unpublished paper. U.S. Immigration and Naturalization Service.
World Bank. 2005. World development indicators 2005. Washington, DC: World Bank. Available on CD-ROM.