Using Matched Survey and Administrative Data to Estimate Eligibility for the Medicare Part D Low-Income Subsidy Program
Social Security Bulletin, Vol. 70, No. 2, 2010 (released May 2010)
This article uses matched survey and administrative data to estimate, as of 2006, the size of the population eligible for the Low-Income Subsidy (LIS), which was designed to provide "extra help" with premiums, deductibles, and copayments for Medicare Part D beneficiaries with low income and limited assets. We employ individual-level data from the Survey of Income and Program Participation and the Health and Retirement Study to cover the potentially LIS-eligible noninstitutionalized and institutionalized populations of all ages. The survey data are matched to Social Security administrative data to improve on potentially error-ridden survey measures of income and program participation. Our baseline estimate, based on the matched data, is that about 12 million individuals were potentially eligible for the LIS as of 2006. A sensitivity analysis indicates that the use of administrative data has a relatively small effect on the estimates, but does suggest that measurement error is important to account for.
Erik Meijer and Pierre-Carl Michaud are economists at the RAND Corporation's Santa Monica office; Lynn Karoly is a senior economist at RAND's Washington office.
Acknowledgments: We would like to thank James Sears, Paul Davies, Lionel Deang, Howard Iams, and Kalman Rupp from SSA for valuable input on this study. Christopher Bollinger (University of Kentucky), David Card (University of California, Berkeley), Guido Imbens (Harvard University), John Karl Scholz (University of Wisconsin, Madison), and David Weir (University of Michigan) served as technical advisors on the project. Our RAND colleagues—Michael Hurd, Geoffrey Joyce, Arie Kapteyn, and Susann Rohwedder provided helpful discussions for which we are grateful, and we appreciate the outstanding programming support provided by Roald Euller, Adria Jewell, and Seo Yeon Hong. This research was supported by contract number SS00-06-60111 from SSA to the RAND Corporation.
Contents of this publication are not copyrighted; any items may be reprinted, but citation of the Social Security Bulletin as the source is requested. The findings and conclusions presented in the Bulletin are those of the authors and do not necessarily represent the views of the Social Security Administration.
Introduction
| CMS | Centers for Medicare and Medicaid Services |
| CPS | Current Population Survey |
| DI | Disability Insurance |
| HRS | Health and Retirement Study |
| LIS | Low-Income Subsidy |
| MBR | Master Beneficiary Record |
| MEF | Master Earnings File |
| OASI | Old-Age and Survivors Insurance |
| PHUS | Payment History Update System |
| SCF | Survey of Consumer Finances |
| SIPP | Survey of Income and Program Participation |
| SSA | Social Security Administration |
| SSI | Supplemental Security Income |
| SSR | Supplemental Security Record |
The 2003 Medicare Prescription Drug Improvement and Modernization Act added a new prescription drug benefit to the Medicare program known as Part D (prescription drug coverage) as well as the Low-Income Subsidy (LIS) program to provide "extra help" with premiums, deductibles, and copayments for Medicare Part D beneficiaries with low income and limited assets. Although Medicare Part D is administered by the Centers for Medicare and Medicaid Services (CMS), the Social Security Administration (SSA) is responsible for administering the LIS, including outreach, processing applications, determining eligibility, and adjudicating appeals.
As part of a study conducted for SSA, reported more fully in Meijer, Karoly, and Michaud (2009), we aimed to estimate the size of the LIS-eligible population as of 2006.1 Such an estimate can be used to determine an upper bound on the number of program participants and to estimate take-up rates based on actual participation. In this article, our estimation approach is featured, which employs survey data matched to administrative data in order to provide the best available estimate. One of the goals of this article, relative to the larger study on which it is based, is to highlight the ability to use matched survey/administrative data for this type of analysis and to report the sensitivity of our results compared with using only survey data.
As shown in Chart 1, as of 2006 when the Medicare Part D program went into effect, eligibility for the LIS first required enrollment in Medicare Part D. However, we focus on generating an estimate that captures the potentially LIS-eligible population because we count as eligible those individuals who are not enrolled in Medicare Part D, but are otherwise eligible for the LIS, even though Part D enrollment is a prerequisite to LIS eligibility. In addition, consistent with the eligibility rules shown in Chart 1, we distinguish between (1) automatic eligibility for the LIS, which affects those persons who are potentially eligible for the full LIS because they are enrolled in the Supplemental Security Income (SSI) program, in Medicaid (dual-eligibles), or in a Medicare Savings program and (2) nonautomatic eligibility for the LIS, which affects those persons who qualify for a full or partial subsidy based only on meeting income and resource (asset) criteria (known as direct eligibility).
Eligibility for the LIS under Medicare Part D, as of 2006
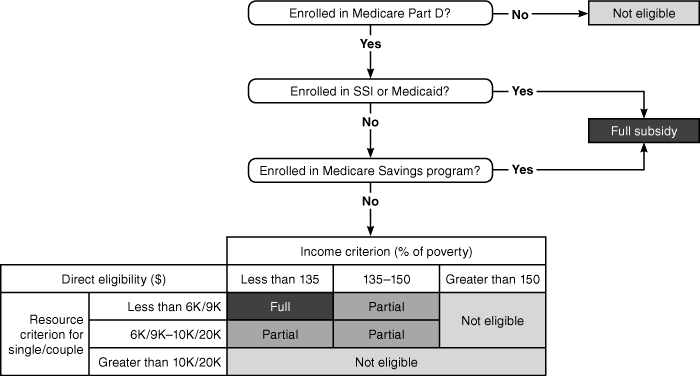
| Direct eligibility ($) | Income criterion (% of poverty) | |||
|---|---|---|---|---|
| Less than 135 | 135–150 | Greater than 150 | ||
| Resource criterion for single/couple | Less than 6K/9K | Full | Partial | Not eligible |
| 6K/9K–10K/20K | Partial | Partial | Not eligible | |
| Greater than 10K/20K | Not eligible | Not eligible | Not eligible | |
To achieve our objective, the ideal data source would provide information on the Medicare population, which includes the noninstitutionalized and institutionalized populations (the latter includes those in nursing homes) and includes both those eligible because they are aged 65 or older as well as those younger than age 65 who are eligible for Medicare because they have a qualifying disability. The data source would have information on participation in the programs that confer automatic eligibility (for example, SSI, Medicaid, Medicare Savings programs) as well as information to determine direct eligibility (measures of income and resources that match those used in the eligibility determination process). As might be expected, this ideal data source does not exist, either in the form of survey or administrative data.
Instead, we employ individual-level survey data from the Survey of Income and Program Participation (SIPP) and the Health and Retirement Study (HRS) to cover the potentially LIS-eligible noninstitutionalized and institutionalized populations of all ages. The survey data are matched to Social Security administrative data to improve on potentially error-ridden survey measures of income components (for example, earnings, recipient payments from SSI, and benefits from the Old-Age and Survivors Insurance (OASI) and Disability Insurance (DI) programs) and program participation (for example, in SSI, Medicare, or Medicaid/Medicare Savings). The administrative data include the Master Beneficiary Record (MBR), the Payment History Update System (PHUS), the Master Earnings File (MEF), and the Supplemental Security Record (SSR). The survey data are the source of information on asset components as well as the income components (for example, private pensions) not covered in the administrative data.
Although this approach can largely support our data needs, other methodological challenges are introduced as a result. For example, because the SIPP and HRS are longitudinal data sources, selective attrition over time may lead to an unrepresentative sample. Likewise, there may be selective attrition in the sample because of nonmatches between the survey and administrative data. Finally, some of the survey data on income or assets that do not have a counterpart in administrative data may be measured with error, and the available income measures may not exactly replicate the constructs used by SSA for eligibility determination.
As shown in Table 1, several other estimates of the size of the LIS-eligible population are available, starting with an estimate of 14.2 million eligibles among Medicare Part B enrollees as of 2006, according to preliminary estimates provided by the Congressional Budget Office (2004) and concluding with an estimate of 12.5 million eligibles as of 2008, according to CMS (2008). The estimates that pertain to 2006 range from 14.2 million to 11.6 million. Table 1 shows that these estimates have largely relied on the SIPP—sometimes matched with administrative data. The studies differ in whether the estimates apply to the entire eligible population or only the noninstitutionalized population (that is, those in nursing homes and other institutional settings are not counted, as is the case with the SIPP sample frame). None of the studies accounted for attrition or selective matching, and they differ in the extent to which they account for the final LIS eligibility rules.
| Study | Methodology | Results: Estimated LIS-eligible population | |||||
|---|---|---|---|---|---|---|---|
| Survey data source(s) | Administrative data source(s) | Population covered | Account for attrition or selective matching | Final LIS eligibility rules applied | Number, in millions (year) | Percent | |
| Congressional Budget Office (2004) | SIPP (2001 panel, waves unknown) | Medicaid, MCBS | Noninstitutionalized and institutionalized Medicare Part B enrollees a | No | No | 14.2 (2006) | 35.5 |
| McClellan (2006) and CMS (2007, 2008) | SIPP (panel unknown) CPS (year unknown) | None | Noninstitutionalized and institutionalized | No | Yes | 13.2 (2006) 13.2 (2007) 12.5 (2008) |
-- |
| Rice and Desmond (2005, 2006) | SIPP (2001 panel, waves 4–6) | None | Noninstitutionalized only | No | Yes, but resource measure appears to be incomplete | 11.6 (2006) | 29.6 |
| SOURCE: Authors' tabulations from cited studies. | |||||||
| NOTES: MCBS = Medicare Current Beneficiary Survey; -- = data not available. | |||||||
| a. About 94 percent of Medicare beneficiaries were enrolled in Part B. | |||||||
The estimates we generate advance those previously available in the following ways, by—
- employing both the SIPP and HRS to cover the noninstitutionalized and institutionalized populations of all ages potentially eligible for the LIS;
- adjusting sample weights to account for panel data attrition and selective matching of survey and administrative data;
- using matched administrative data to improve on potentially error-ridden survey measures of income and program participation; and
- constructing measures of income and resources that replicate as closely as possible the constructs used to determine LIS eligibility.
In addition, we perform a sensitivity analysis to determine how robust results are to variation in the methodology.
In the next section, we begin by providing detail on the sources of survey and administrative data on which we rely. In the third section, we discuss our approach for attaining the methodological advances highlighted earlier. Our findings are detailed in the fourth section. The baseline estimate, based on the matched data, is that about 12 million individuals were potentially eligible for the LIS as of 2006. A sensitivity analysis indicates that the use of administrative data has a relatively small effect on the estimates, but does suggest that measurement error is important to account for. The estimate of the size of the LIS-eligible population is more sensitive to the relative weight placed on the two survey data sources, rather than the choice of methods applied to either data source. The final section concludes the article.
Sources of Survey and Administrative Data
As noted in the previous section, no single source of survey or administrative data provides the information needed to estimate the LIS-eligible population accounting for both the noninstitutionalized and institutionalized populations. Administrative data sources do not include the full range of income, asset, and living arrangements information required to determine eligibility for the LIS.2 No single survey data source covers the eligible population of interest, and these data contain potentially error-ridden measures of the required income, assets, and program participation information. By using two survey data sources—the SIPP and HRS—we cover the relevant population of interest with survey measures that can potentially be used to determine LIS eligibility. By matching the SIPP and HRS to administrative data sources, we can use the administrative measures of income components and program participation that are arguably error free in place of the equivalent survey measures.
Table 2 summarizes the two sources of survey data and the four sources of administrative data used in the analysis, the universe covered by each source, the key variables used, any remarks about the data, and the particular usage in the analysis methodology (detailed in the next section). For the SIPP, we rely on data from the 2004 SIPP panel, waves 1–10, which provides data through the end of 2006. The SIPP consists of a continuous series of nonoverlapping nationally representative panels with survey waves that are 4 months apart and a total duration that has typically been 3–4 years (Westat 2001). It is a multistage, stratified sample of the U.S. civilian noninstitutionalized population. Because the SIPP includes individuals aged 15 or older, it contains information about those who are eligible for Medicare through disability, but are younger than the youngest HRS-sampled individuals (who were age 53 in 2006). On the other hand, the SIPP sample does not contain information about individuals in nursing homes. The 2004 SIPP panel included a total of 46,500 households in the initial wave. However, starting with wave 9, the SIPP sample size was reduced by about half because of budget cuts. This sample-size reduction affects the monthly data we have for calendar year 2006. In addition to data from the core, we also rely on several topical modules, including wealth information collected in wave 3 (administered October 2004–January 2005) and wave 6 (administered October 2005–January 2006).
| Data source | Universe | Key variables | Remarks | Usage and year of data |
|---|---|---|---|---|
| Survey data | ||||
| 2004 SIPP | Civilian, noninstitutionalized | Program participation (Medicare, Medicaid, SSI), earnings, benefits, assets, and liabilities | Oversamples low incomes to obtain a better picture of program participation |
|
| HRS | Civilian (including those in retirement homes), aged 50 or older | Program participation (Medicare, Medicaid, SSI), earnings, benefits, assets, and liabilities | Follows individuals into nursing homes |
|
| Administrative data | ||||
| LIS application and decision files | LIS applicants (excludes those automatically enrolled) | Income (various categories), resources (various categories), expectation to use funds for funeral/burial | None |
|
| MBR/PHUS | OASI and DI applicants/ beneficiaries | Benefits, disability, Medicare beneficiary, and Medicaid/Medicare Savings beneficiary | None |
|
| SSR | SSI applicants | SSI recipient and SSI income | None |
|
| MEF | All W-2 forms, 1040 Schedule SE | Detailed earnings data | None |
|
| SOURCE: Authors' tabulations from documentation of the various data sources. | ||||
The HRS is a multipurpose, longitudinal household survey providing extraordinarily rich data that are representative of the U.S. population older than age 50 (National Institute on Aging 2007). It consists of a national area probability sample of U.S. households, with supplemental samples of Mexican Americans, African Americans, and Floridians. At baseline, respondents were selected from the community-dwelling population (including retirement homes, but not nursing homes). However, in subsequent waves, respondents were followed even if they entered an institution. The initial HRS wave took place in 1992 and sampled individuals born in the 1931–1941 period and their spouses (of any age). Over time, additional cohorts have been added so that by 1998, the HRS was representative of the U.S. population older than age 50. Respondents in each cohort have been interviewed every 2 years. Note that, unlike the SIPP, the HRS sample does not include individuals who are eligible for Medicare because of disability, but who are younger than age 53. On the other hand, because the HRS follows respondents when they enter institutions, the HRS covers individuals in nursing homes quite well.3
We use the HRS public-use files created by RAND, a user-friendly version of a large subset of the HRS variables (St. Clair and others 2008) and base our analysis on the 2006 wave, which included about 18,000 respondents, of whom 11,000 were aged 65 or older. One of the virtues of the HRS is the high quality of the data on income (for the previous calendar year) and assets (current), both collected through questions that ascertain amounts for disaggregated categories. The level of quality is due largely to the design of the questionnaire, in which unfolding brackets are used (a feature not employed in the SIPP), which allow respondents to give interval answers if they are not willing or able to give exact amounts. This leads to much lower item nonresponse rates. Moreover, because of these brackets, imputations are much more precise (Juster and Smith (1997); Hurd, Juster, and Smith (2003)). For this study, we rely on the high-quality imputations of income and wealth, based on the unfolding brackets, made available in the RAND HRS files.
As shown in Table 2, in addition to the SIPP and HRS, we rely on four primary sources of administrative data, which include the following key information:4
- LIS application and decision files. Include data from the LIS application forms (that is, responses regarding income and assets required for eligibility determination) and the corresponding decisions about whether the subsidy was awarded. These data are our primary source of information about whether individuals expect to use some of their assets for funeral or burial expenses because this information is not in the SIPP or HRS.
- MBR and PHUS. Provide information on OASI/DI applicants and beneficiaries, including dollar amounts received and whether Medicare premiums are paid by a state agency.
- SSR. Covers SSI applicants and recipients with data on dollar amounts received, including federal and state supplements.
- MEF. Provides information on wages and salaries (from W-2s) and self-employment income (from 1040 Schedule SEs).
In the case of the SIPP, as SSA contractors with Census Bureau special sworn status, we had access at a secure SSA facility to administrative data that had been matched to the 2004 SIPP panel. For the HRS, under an agreement between SSA and HRS officials, with respondent permissions obtained in the 2004 HRS and a data protection plan to safeguard against disclosure of sensitive information, we had access at our premises to the restricted HRS data that had been matched to administrative data through 2003.
Methods
Estimating the size of the LIS-eligible population presents a number of methodological challenges that need to be addressed. First, possible biases that result from using later waves of the 2004 SIPP and HRS panel data need to be accounted for, where nonrandom attrition may mean the sample is no longer representative of the population covered in the survey frame. In addition, because not all observations will be successfully matched between the survey and administrative data, potential distortions in the representativeness of the matched sample need to be accounted for. Second, we need to account for possible measurement error in the survey data on income, assets, and program participation—the key determinants of LIS eligibility. Third, an algorithm is needed to replicate the LIS eligibility determination rules based on the available survey and administrative data, which do not contain the full set of information used by SSA to determine eligibility. We describe our approach to addressing these three issues in the remainder of this section. As a supplement to the discussion, Charts 2 and 3 provide schematic representations for our approach to using the SIPP and HRS, which vary because of the differences in the nature of the available survey and administrative data.
Methodological approach to using the SIPP
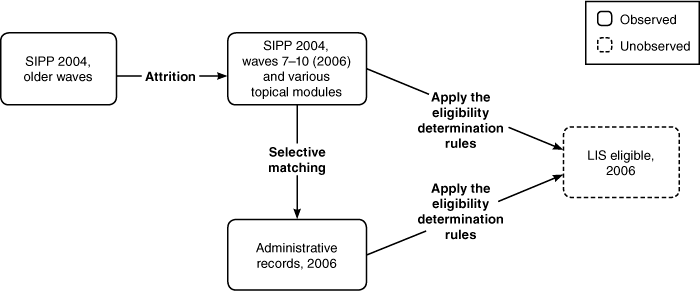
Text description for Chart 2.
Methodological approach to using the SIPP
Chart 2 provides a schematic representation of the methodological approach to using the SIPP. In particular, we use waves 7 to 10 of the 2004 panel, covering calendar year 2006 as well as several topical modules. We account for potential bias from nonrandom attrition from the baseline wave and nonrandom attrition when matching to administrative data records in 2006. We then apply our algorithm for the LIS eligibility determination rules to the 2006 SIPP survey data and 2006 matched administrative data to estimate the number of LIS-eligibles in 2006.
Methodological approach to using the HRS
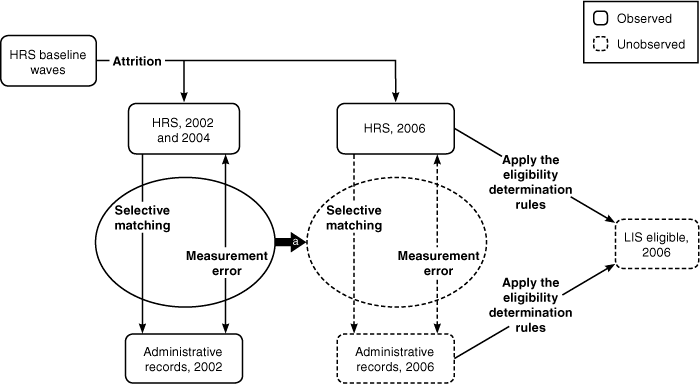
Text description for Chart 3.
Methodological approach to using the HRS
Chart 3 provides a schematic representation of the methodological approach to using the HRS. In particular, we use the 2002 and 2004 HRS matched to administrative records for 2002. We account for potential bias because of nonrandom attrition when matching to the administrative data as well as measurement error in Medicaid/Medicare Savings status. Because we do not observe administrative records for 2006, we assume the same conditional relationship observed in the matched survey/administrative data from 2002 to impute equivalent administrative survey data measures. We also account for nonrandom attrition from the baseline HRS wave when analyzing the 2002, 2004, and 2006 waves of HRS data. We then apply our algorithm for the LIS eligibility determination rules to the 2006 HRS survey data and 2006 imputed administrative data to estimate the number of LIS-eligibles in 2006
Reweighting to Account for Panel Data Attrition and Data Matching
Our SIPP analytic survey sample, from waves covering calendar year 2006, consists of only 29 percent of eligible respondents based on the baseline sample. A large part of the drop in sample size is due to the reduction of the sample by about 50 percent in 2006 because of a budget cut. The remainder of the sample loss results from panel attrition. About 87 percent of the respondents in the analytic survey sample are then available in our matched survey/administrative sample.5 For the HRS, the panel attrition rate was about 18 percent in 2006 (so 82 percent of eligible respondents are in the sample). We use 2002 matched administrative/HRS data for modeling; in this data set, the attrition rate is 25 percent, and the match rate is 54 percent. The relatively low match rate is largely the result of a low percentage of respondents giving permission to match their records. Thus, in both data sources, our analytic samples—based on data from later waves of the two longitudinal studies and matched survey/administrative data—are much smaller than the original samples, and there is considerable scope for biases that are due to selective attrition and matching.
Problems that are the result of attrition and selection introduced by matching administrative records to survey data can be conceptualized using the missing-data framework (Little and Rubin 2002). In the case of attrition, we observe data collected from a respondent when he or she participates in a given wave of the survey. Data of interest are missing when the respondent does not answer. Similarly, if it is not possible to link the survey data for some respondents to administrative records, data from those respondents are missing. The key issue is that the sample of respondents with nonmissing data may have different characteristics from those of the relevant population of interest, thereby biasing any estimates based on the available sample.
Our general approach, following Kapteyn and others (2006), is to develop weights to correct for selective panel attrition based on baseline observables, which relax the potentially restrictive assumptions underlying the survey-provided weights. In particular, we estimate probability models of survey participation as a function of baseline characteristics and adjust survey weights accordingly. Because the baseline characteristics used are more comprehensive than just race, ethnicity, age, and sex—as used in survey weights—they allow us to weight respondents with unfavorable characteristics (from the viewpoint of survey participation) more heavily than those with favorable characteristics. We refer to these weights as inverse probability weights (IPWs).
In particular, for the 2004 SIPP panel, we rely on data from waves 1–4 and 7–10, which cover the calendar months of 2004 and 2006 (full data from waves 2 and 3 and partial data from waves 1 and 4 cover 2004, and full data from waves 8 and 9 and partial data from waves 7 and 10 cover 2006). For the SIPP, we also use supplementary data from topical modules (TMs) administered with waves 3–7, which provide information on assets and liabilities (TM3 and TM6), annual income and taxes (TM4 and TM7), and health status (TM3, TM5, and TM6). For the HRS, we use the 2002, 2004, and 2006 waves. As detailed in Meijer, Karoly, and Michaud (2009), we find that the differences induced by selection on observables in both the SIPP and HRS are minor and that weighting based on IPWs and survey weights tend to give very similar results. For the HRS, the attrition-corrected weights have the advantage of providing sampling weights for those persons in nursing homes as of 2004 and 2006 (based on their baseline weights and the IPWs) because weights are otherwise not available in the HRS for those who transition to nursing homes.
Our approach for correcting for selective matching is similar to that followed for selective attrition. Thus, we estimate models of the probability of a nonmatch and use the models to generate IPWs that correct for selectivity in the sample with matched data. In the case of the HRS, the match is possible for those respondents who provided permission as part of the 2004 HRS wave. However, not all respondents gave permission to the HRS to match their records to administrative data. Furthermore, some respondents gave permission, but provided a wrong Social Security number or no number at all, or the match failed for another reason (typically unknown). For the SIPP, only a very small percentage of respondents refused to give permission for matching, so, essentially, a failure to match will arise only for other reasons.
In the case of the HRS, as discussed more fully in Meijer, Karoly, and Michaud (2009), our results are consistent with those of previous studies on the match available for the 1992 wave, which showed little bias (see, for example, Olson (1999) and Haider and Solon (2000)). Although some characteristics, such as education, wealth, and labor force experience, differ in matched and unmatched samples, the effects are too small to generate large problems in analyzing data in the matched samples. A similar finding holds for the SIPP. Although the potential bias from selective attrition and matching appears to be small, we use the attrition- and matching-corrected weights constructed to generate our preferred estimates of the LIS-eligible population.
After comparing preliminary results from the attrition analyses with population statistics from the Census Bureau, we were concerned that the SIPP does not adequately record mortality and nursing home entry of respondents when they are not found in later waves. Hence, some respondents who are no longer in the SIPP sample frame are misclassified as attritors, whereas, in fact, they are no longer in the target population of the SIPP. The result of this is an overestimation of the population size in the SIPP when the attrition-corrected weights are used. To correct for this, we performed a final reweighting of the SIPP toward demographic distributions that were obtained from the January 2006 Current Population Survey (CPS). For consistency, we performed a similar reweighting of the HRS, using the CPS for the noninstitutionalized population and a combination of the 2004 wave of the National Nursing Home Survey and distributions for 2006 as published by CMS for nursing home residents.
Correcting for Measurement Errorin Survey Data
It is well known that survey data, especially measures of income, wealth, and program participation, tend to be subject to systematic measurement error (see, for example, Bound, Brown, and Mathiowetz (2001); Czajka, Jacobson, and Cody (2003); Card, Hildreth, and Shore-Sheppard (2004); and Davern, Klerman, and Ziegenfussi (2007)). The expected underreporting of income and wealth would lead to overestimation of the number of individuals eligible for the LIS. Likewise, the expected underreporting of Medicaid enrollment and enrollment in other programs that ensure eligibility for LIS would lead to underestimation of the number of LIS-eligibles or, more importantly (given that these individuals would quite likely have low incomes and resources), misclassification as being nonautomatically eligible for the LIS instead of being deemed automatically eligible.
Administrative records are typically assumed to be without measurement error. Matching the survey data with administrative records then serves multiple purposes. First, if the administrative data pertain to the time period of interest, these data can replace (partly) the survey data and be used directly in determining eligibility. Second, in case the administrative data are available only for a different time period or only for a nonrepresentative subset of the surveyed individuals, eligibility estimates for this different universe, computed from the administrative data, can be compared with corresponding estimates from the survey data. Because that universe differs from the universe of interest, neither of these estimates is then of interest by itself, but the extent to which the two sets of estimates differ gives an indication of the consequences of measurement error if only survey data were used to compute estimates. Third, if the result of this comparison exercise is that measurement error leads to unacceptable distortions, then the observed relationships between survey and administrative data can be used to estimate the conditional distribution of the true values, given the survey data.
We call this a measurement-error model because the typical case is to estimate the distribution of the true value of a certain characteristic (for example, earnings) given an error-ridden survey value of the same characteristic, but the principle applies more generally to the distribution of a variable T that is in the administrative data conditional on the values of survey variables, collected in the vector S, which are observed in the survey data. Note that the direction of the model is reversed from the typical measurement-error model as, for example, discussed extensively in Wansbeek and Meijer (2000) and that we do not assume causality, but are interested only in the conditional distribution. Once the parameters of such a conditional distribution are estimated, eligibility estimates for the universe of interest can be obtained by simulating (imputing) from this conditional distribution. With this framework, we address three potential types of measurement error in our data.
Mismeasured Medicaid beneficiary status. Because Medicaid (and Medicare Savings) beneficiary status makes one automatically eligible for the full LIS subsidy, measurement error in this area will have a noticeable impact on the eligibility estimates, especially on the categorization into automatic eligibility and nonautomatic eligibility. The impact on the total number of eligibles is likely to be considerably less because most of the beneficiaries involved will otherwise be eligible according to their incomes and resources. Notably, Medicaid beneficiary status is known to be severely underreported in the SIPP and other surveys, such as the CPS (Card, Hildreth, and Shore-Sheppard (2004); Davern, Klerman, and Ziegenfussi (2007)).
The use of matched Social Security administrative data addresses this issue directly. In both the administrative data matched to the HRS and the administrative data matched to the SIPP, there is a variable indicating whether the state Medicaid agency pays for the Medicare Part B premiums. This payment is made whenever an individual is both a Medicare Part B beneficiary and a Medicaid or Medicare Savings beneficiary. Almost all Medicare beneficiaries have both Part A and Part B coverage, and, among Medicaid or Medicare Savings beneficiaries, this coverage must be essentially 100 percent because the Part B premiums are paid by Medicaid. Hence, the variable also identifies whether an individual is a Medicaid or Medicare Savings beneficiary, provided that he or she is even eligible for Medicare—the population that is potentially eligible for the LIS. This method has been applied previously by the General Accounting Office (2004).
For the SIPP-based analyses, administrative data for 2006 are employed, so we can simply use the administrative variable in place of the survey variable. For the HRS-based analyses, the same approach cannot be used because we have administrative data only up to 2003. However, preliminary estimates showed that the estimates of the percentage automatically eligible for the LIS for the common subpopulations were considerably lower in the HRS compared with the SIPP. We viewed this as evidence of misreporting of Medicaid/Medicare Savings beneficiary status in the HRS. Therefore, we have estimated a model (using 2002 data) that predicts true (administrative) Medicaid/Medicare Savings beneficiary status as a function of the corresponding survey variable and other explanatory variables from the HRS, such as sociodemographics, income, and resources.6 We then use the model to impute Medicaid/Medicare Savings beneficiary status in the 2006 HRS data. Counter to our expectation, Medicaid/Medicare Savings beneficiary status tended to be overreported in the HRS according to the model as well as in the 2002 data on which it is based.
To assess the impact of the Medicaid undercount in the SIPP or HRS, we can then compare estimates of the number of LIS-eligibles based on survey data with those based on administrative data for the same year and population. Given the matched records, we can even isolate the effect of the Medicaid undercount by comparing estimates using the administrative Medicaid variable with estimates using the corresponding survey variable, keeping all other variables the same. The results are reported in the next section as part of the sensitivity analysis.
Measurement error in income measures. Aside from the Medicaid undercount, income-measurement error is another stylized fact of survey data. Several income components are measured in the administrative data: earnings and income from Social Security (Old-Age, Survivors, and Disability Insurance (OASDI)) and SSI. In the case of the SIPP data, these administrative measures are available for 2006 so, again, we use the administrative measures in place of the survey data. For the HRS, however, as with Medicaid status, we only have administrative data for these income measures as of 2003. Thus, we put some effort into estimating measurement-error models for the HRS for these three income components (for example, earnings measurement-error models along the lines of that in Brownstone and Valletta (1996)), but our efforts did not lead to satisfactory models. Moreover, preliminary comparisons of pseudo-eligibles in the 2002 HRS (that is, estimating who would have been eligible if the LIS had existed in 2002, adjusting the 2006 income and resource thresholds backward in time to account for inflation) with and without matching administrative data to the survey showed small differences. Given that this did not appear to be an important source of bias, we did not pursue measurement-error corrections in the HRS.7
For the income components for which we do not have administrative data, for example, pension income and rental income, we cannot assess whether there is measurement error and whether it has a noticeable impact on the eligibility estimates. There appears to be no alternative for assuming that these income components are measured without error. This holds for both the HRS and SIPP.
Measurement error in wealth measures in the SIPP. Czajka, Jacobson, and Cody (2003) have done an extensive study of measurement error in wealth measures in the SIPP. Because detailed administrative data on wealth components are not available, this analysis was done primarily by comparing the distributions of SIPP wealth measures with the corresponding distributions in the Survey of Consumer Finances (SCF), which is generally considered the best source of wealth data in the United States. Czajka and colleagues conclude that the SIPP measure of aggregate wealth is only half of the SCF measure of aggregate wealth (p. 24). This is a huge difference and a potential source of large upward biases in the estimates of the number of LIS-eligibles. However, it is not immediately clear whether the authors' conclusions regarding a late wave of the 1996 panel carry over to the waves of the 2004 panel that we use, as a number of wealth components not available in the 1996 panel were included in the 2004 panel. Moreover, the mismeasurement of wealth in the SIPP pertains largely to the top of the distribution (for example, families with net worth greater than $2 million). Clearly, such families would not be eligible for the LIS, so measurement error in wealth in this segment of the distribution is less of a concern.
A recent analysis by Scholz and Seshadri (2008) suggests, however, that there is more cause for concern about measurement error in the SIPP wealth data at the lower tail of the distribution. Their study provided detailed comparisons of asset distributions between the SCF (multiple waves) and the SIPP (multiple panels and waves). Most importantly for our purposes, they find that, in the SIPP (in 2003), a much lower percentage of individuals in the bottom income quintile have positive financial assets than do those in the SCF and, among those with nonzero amounts, the median financial assets are substantially lower in the SIPP than in the SCF.
There are a few wealth components in the SIPP that are not measured well and that could influence our estimates: interest-earning assets besides those held at financial institutions, other real estate, business equity, and rental property. We have done limited sensitivity analyses including and excluding some of these components from the HRS resource amounts, where wealth estimates are considered to be more accurate. Including the other real estate (net value) component increases the number of individuals who are ineligible for the LIS because of their resources by about 2.6 percent compared with completely excluding it; including the business property (net value) component increases the number by 1.1 percent; and including both resource components together increases the number by 3.7 percent. These are upper bounds because measurement error will not reduce these components to zero for all respondents. Moreover, a sizable fraction of the individuals who cross the threshold in this way may not be eligible according to their income anyway, thereby further diminishing the potential impact of measurement error in these wealth components in the SIPP. This issue is considered again in the sensitivity analysis reported in the next section.
Implementing the LIS Eligibility Determination Rules
For purposes of estimating the potentially LIS-eligible population, we implement a computer algorithm that replicates, as closely as possible, the eligibility determination rules, shown schematically in Chart 1, that correspond to the LIS regulations (see Meijer, Karoly, and Michaud (2009) for more detail). Some of the details of the eligibility determination rules—such as who in the household is counted for purposes of determining family size and what income and resource components are included or excluded—are complex. For example, the income concept uses a simplified SSI methodology, which includes only the income of the Medicare beneficiary and his or her spouse and is based on annual income. As of 2006, income disregards (that is, income amounts that are deducted from the measure of countable income) included the first $240 of income plus the first $780 of earned income and half of all remaining earned income. Other income components that are not counted include food stamp benefits; home energy, housing, or disaster assistance; Earned Income Tax Credit payments; victim's compensation; and scholarships and educational grants. The family size count may include other family members beyond the beneficiary and his or her spouse, if the other family members receive more than half of their support from the beneficiary.
In the case of assets, resources that do count toward the threshold include real estate other than the primary residence; cash and bank accounts; stocks, bonds, and mutual funds; and individual retirement accounts (IRAs). The measure of resources does not include the primary residence, personal possessions, vehicles, property needed for self-support, resources up to $1,500 of the cash value of life insurance policies for each individual, and resources up to $1,500 (single) or $3,000 (couple) expected to be used for funeral or burial expenses.
The algorithm establishes Medicare beneficiary status, Medicaid/Medicare Savings beneficiary status, and SSI receipt and computes estimates of countable income and countable resources. In particular, the eligibility algorithm first computes eligibility indicators for different criteria separately and then combines them in an overall eligibility indicator. For all criteria, individuals who are not Medicare beneficiaries (Part A or B) are ineligible, so the eligibility criteria indicators are restricted to Medicare beneficiaries. The first two indicators show automatic eligibility because of being either an SSI recipient or a Medicaid/Medicare Savings beneficiary. These indicators are simply equivalent to the SSI and Medicaid/Medicare Savings indicators, given the Medicare beneficiary status. The next two indicators express how income and resources relate to the respective criteria for direct eligibility for a full or partial subsidy (see Chart 1). In this way, not only is the total number of eligibles computed, but so is the source of eligibility (that is, automatic versus direct) and the extent of the subsidy (that is, full versus partial).
In some cases, the data required to match the constructs specified in the regulations are not available in either the SIPP or HRS. Thus, we either adopt methods to approximate those constructs or consider sensitivity analyses to different assumptions. For example, neither the SIPP nor HRS contain a measure of the amount of resources the respondent plans to use for funeral and burial expenses. Thus, in computing the resource indicator, the $1,500 (singles)/$3,000 (couples) exclusion for funeral and burial expenses is subtracted from the measure of countable resources before deductions, assuming that everyone expects to need at least this amount for his or her own funeral and/or burial.8
Baseline Results and Sensitivity Analyses
Using the eligibility algorithm, we determine the potential eligibility for the LIS of each individual in either the HRS or SIPP sample. The number of potentially eligible individuals is then a weighted sum of the indicator variable that is 1 if the individual is classified as eligible and 0 otherwise, using the sampling weights that we have constructed that adjust for panel attrition and selective matching. Analogously, we can estimate the number of individuals who are automatically eligible for the full subsidy, the number of individuals who are nonautomatically eligible for the full subsidy, and the number of individuals who are eligible for a partial subsidy only, by using indicator variables for these categories instead of the overall eligibility indicator variable.
Table 3 shows how we use the SIPP and HRS to generate an estimate for the population of interest, stratified by age (three groups) and institutionalization status (two groups). As shown in the table, our approach combines estimates from the SIPP and HRS, in some cases relying on only one data source or the other. For example, the SIPP is the only source of information on the noninstitutionalized population aged 52 or younger (one cell). The HRS is the only source of information on the nursing home population aged 53 or older (two cells). Both data sources cover the noninstitutionalized population aged 53 or older (two cells). Neither data source provides information on the nursing home population under age 53 (one cell).9 For those cells for which both data sources are available, the results we present for the baseline estimate are based on the average of the separate estimates for each data source. The estimates for the marginal totals by age group or by institutionalization status and the grand total are based on summing within columns or across rows.
| Population group | Age group | Total | ||
|---|---|---|---|---|
| 0–52 | 53–64 | 65 or older | ||
| Noninstitutionalized population | SIPP | SIPP/HRS average | SIPP/HRS average | Sum across age groups |
| Nursing home population | -- | HRS | HRS | Sum across age groups |
| Total population | SIPP | Sum within age group | Sum within age group | Sum within total |
| SOURCE: Authors' analysis. | ||||
| NOTE: -- = data not available. | ||||
In the results that follow, we report robust linearization standard errors (computed in Stata) for the point estimates that take into account sampling error that arises from the complex survey designs in the SIPP and HRS (that is, stratification, clustering, and oversampling of some demographic groups).10 Presented next are our baseline results as well as a sensitivity analysis that assess the implications of using the matched survey/administrative data.
Baseline Estimates
Table 4 reports results, stratified by age group, for the baseline estimated number of Medicare beneficiaries, with a breakdown by those estimated not to be LIS-eligible and those estimated to be LIS-eligible.11 We further disaggregate those estimated to be eligible for the LIS by the eligibility pathway and degree of subsidy. Panel A reports outcomes as numbers (in millions); panel B reports outcomes as percentage distributions. Estimated standard errors are reported for the absolute figures. In panel B, we also disaggregate the group that is estimated to be ineligible for the LIS by whether income only is too high, resources only are too high, or both income and resources are too high.
| Measure | Age group | Total | ||
|---|---|---|---|---|
| 0–52 | 53–64 | 65 or older | ||
| Panel A: Number (millions) | ||||
| Total Medicare beneficiaries | 3.465 (0.255) |
3.271 (0.165) |
35.297 (0.835) |
42.033 (0.998) |
| Not eligible for LIS | 0.697 (0.088) |
1.692 (0.122) |
27.406 (0.693) |
29.795 (0.737) |
| Eligible for LIS | 2.768 (0.228) |
1.580 (0.115) |
7.891 (0.269) |
12.238 (0.425) |
| Automatically eligible, full subsidy | 2.035 (0.191) |
0.910 (0.084) |
3.972 (0.174) |
6.917 (0.290) |
| Other eligible, full subsidy | 0.560 (0.093) |
0.541 (0.066) |
2.720 (0.126) |
3.821 (0.185) |
| Other eligible, partial subsidy | 0.173 (0.045) |
0.129 (0.056) |
1.199 (0.082) |
1.500 (0.108) |
| Panel B: Percentage distribution | ||||
| Total Medicare beneficiaries | 100.0 | 100.0 | 100.0 | 100.0 |
| Not eligible for LIS | 20.1 | 51.7 | 77.6 | 70.9 |
| Income only too high | 5.7 | 17.9 | 15.8 | 15.1 |
| Resources only too high | 5.5 | 7.2 | 9.8 | 9.3 |
| Income and resources too high | 8.9 | 26.6 | 52.1 | 46.5 |
| Eligible for LIS | 79.9 | 48.3 | 22.4 | 29.1 |
| Automatically eligible, full subsidy | 58.7 | 27.8 | 11.3 | 16.5 |
| Other eligible, full subsidy | 16.2 | 16.5 | 7.7 | 9.1 |
| Other eligible, partial subsidy | 5.0 | 3.9 | 3.4 | 3.6 |
| SOURCE: Authors' calculations using SIPP, HRS, and Social Security administrative data. | ||||
| NOTES: The sample sizes are 26,354 persons for the SIPP, 4,727 of whom are Medicare beneficiaries and 16,060 persons for the HRS, 10,725 of whom are Medicare beneficiaries. | ||||
| Standard errors are in parentheses. | ||||
According to these estimates, as of January 2006, there were 42.0 million Medicare beneficiaries. This is consistent with administrative data from CMS indicating a Medicare beneficiary population of 41.9 million in 2006. Of that total, we estimate that 12.2 million Medicare beneficiaries (or 29 percent) were potentially eligible for the LIS. The estimated standard error is about 0.43 million, so the approximate error bands would be plus or minus 860,000 persons. Of the total number of potentially LIS-eligible persons, most are eligible for a full subsidy, either through automatic eligibility (6.9 million) or by qualifying based on low income and resources (3.8 million). The remaining 1.5 million persons would be eligible for a partial subsidy. The estimate of 6.9 million individuals automatically eligible for the LIS is below the CMS estimate of 7.3 million as of May 2006, a figure based on the CMS Management Information Integrated Repository (CMS 2006). The benchmark of 7.3 million is within the error band of the estimate given in Table 4, however.
Overall, of those persons who are not eligible, most have both income and resources too high (47 percent of the 71 percent of ineligible Medicare beneficiaries). The remainder have either income only too high (15 percent) or resources only too high (9 percent). The disaggregation by age group shows a higher rate of eligibility among Medicare beneficiaries for younger age groups. This is to be expected because those younger than age 65 who are eligible for Medicare qualify as a result of a work-limiting disability, which increases their likelihood of having low income and resources compared with the population aged 65 or older, who qualify for Medicare because of age.
The baseline estimates in Table 4 weight the SIPP and HRS equally for those cells in Table 3 where both data sources are available. For the noninstitutionalized population aged 53 or older—for which an estimate can be obtained using either the SIPP or HRS—Meijer, Karoly, and Michaud (2009) show that the HRS provides a higher estimate of the number of LIS-eligibles in the subgroup aged 53–64 compared with the SIPP (1.6 million versus 1.3 million), whereas the SIPP provides a higher estimate than does the HRS for those aged 65 or older (8.7 million versus 6.1 million).
Given the differences between the SIPP and HRS in the estimate of LIS eligibility for the noninstitutionalized population, we have calculated two alternative baseline estimates of LIS eligibility for the total population. The baseline estimates in Table 4 average the HRS and SIPP estimates when both data sources are available for the same subpopulation (as shown in Table 3). One alternative is to give preference to the SIPP estimates when both data sources are available and use the HRS only when it is the sole source of information for a given subpopulation (that is, the institutionalized population aged 53 or older). The other alternative is to give preference to the HRS when both data sources are available and use the SIPP only for those subpopulations for which it is the only source of information (that is, the noninstitutionalized population younger than age 53). These two extremes will bound the estimates that we reported in Table 4 where we averaged the two data sources.
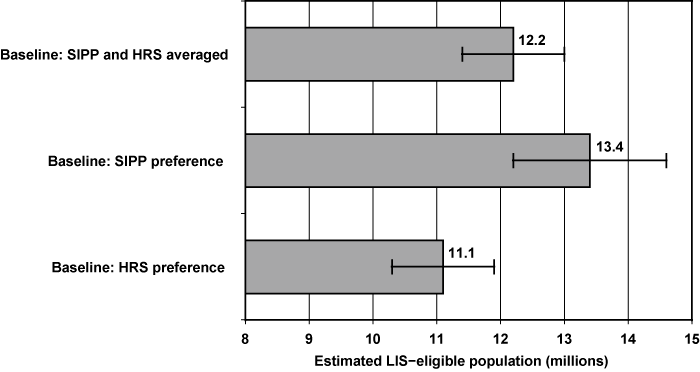
The results for the total number of LIS-eligibles that use the three weighting schemes are plotted in Chart 4. The first bar is based on giving equal weight to the SIPP and HRS when they are both available (consistent with Table 4). The second bar shows the result when the SIPP is given preference, and the third bar shows the result when the HRS is given preference. When the SIPP is treated as the preferred data source, the estimated LIS-eligible population is higher by about 2.3 million persons than when the HRS is treated as the preferred data source, a total of 13.4 million versus 11.1 million. When the standard errors for these estimated figures are used to create 95 percent confidence intervals, the estimates range from a lower bound of 10.3 million LIS-eligibles based on the HRS, to an upper bound of 14.6 million eligibles based on the SIPP, a relatively wide range.
Point estimates and confidence intervals for baseline estimate of potentially LIS-eligible population in 2006, with alternative weighting given to SIPP and HRS estimates
| Estimate | Estimated LIS-eligible population (millions) |
Standard error | Bottom confidence interval | Top confidence interval |
|---|---|---|---|---|
| Baseline: SIPP and HRS averaged | 12.2 | 0.425 | 11.4 | 13.1 |
| Baseline: SIPP preference | 13.4 | 0.620 | 12.2 | 14.6 |
| Baseline: HRS preference | 11.1 | 0.406 | 10.3 | 11.9 |
Sensitivity Analysis
Given the differences in the estimates of LIS-eligibles based on the SIPP and HRS, we explore two possible sources of those differential estimates through a sensitivity analysis.12 We first consider the implications of using administrative data versus survey data because the SIPP estimate is based on administrative data for 2006, whereas the HRS estimate is based on a model-based imputation using earlier administrative data for Medicaid/Medicare Savings coverage and self-reported data on SSI recipient status. The consequences of differential wealth distributions between the SIPP and HRS for our estimates are then considered.
Administrative versus survey data. The differences in the SIPP and HRS estimates may result from the differential use of administrative data in the sources. To assess the sensitivity in using administrative data, we compute alternative estimates based only on survey data, separately for the SIPP and HRS, as part of a sensitivity analysis shown in Table 5. Note that the SIPP estimates in panel A pertain to the noninstitutionalized population, and the HRS estimates in panel B apply to the noninstitutionalized and institutionalized populations aged 53 or older. Thus, the results are not comparable across the panels because they are for different populations. However, within each panel, we can examine the robustness of results to variation in methods and assumptions for that data source. Those results include estimates of the number of Medicare beneficiaries and the number of LIS-eligible persons versus those not eligible. Among those eligible, we show estimates disaggregated by the pathway and degree of subsidy. For each alternative estimate, we show results in absolute numbers (in millions) and as percentages of the Medicare-eligible population.
| Estimate | Medicare beneficiaries | LIS eligibility status | LIS eligibility by type | |||
|---|---|---|---|---|---|---|
| Not eligible | Eligible | Automatic, full subsidy | Other eligible, full subsidy | Other eligible, partial subsidy | ||
| Panel A: SIPP, noninstitutionalized population | ||||||
| S0: 2006, SIPP and Social Security administrative data, CPS reweight | ||||||
| Number (millions) | 40.614 | 27.829 | 12.785 | 7.253 | 3.994 | 1.538 |
| Percent | 100.0 | 68.5 | 31.5 | 17.9 | 9.8 | 3.8 |
| S1: S0 with no Social Security administrative data | ||||||
| Number (millions) | 40.395 | 27.835 | 12.560 | 7.476 | 3.689 | 1.396 |
| Percent | 100.0 | 68.9 | 31.1 | 18.5 | 9.1 | 3.5 |
| S2: S0 with median wealth correction to HRS distribution | ||||||
| Number (millions) | 40.614 | 29.215 | 11.398 | 7.253 | 3.246 | 0.900 |
| Percent | 100.0 | 71.9 | 28.1 | 17.9 | 8.0 | 2.2 |
| Panel B: HRS, population aged 53 or older | ||||||
| H0: 2006, Medicaid/Medicare Savings imputation, CPS reweight | ||||||
| Number (millions) | 38.756 | 30.445 | 8.312 | 4.180 | 2.932 | 1.199 |
| Percent | 100.0 | 78.6 | 21.4 | 10.8 | 7.6 | 3.1 |
| H1: H0 with no Medicaid/Medicare Savings imputation | ||||||
| Number (millions) | 38.756 | 30.350 | 8.406 | 4.053 | 3.087 | 1.267 |
| Percent | 100.0 | 78.3 | 21.7 | 10.5 | 8.0 | 3.3 |
| SOURCE: Authors' calculations using the SIPP, HRS, and Social Security administrative data. | ||||||
| NOTES: Percentages are for the Medicare-eligible population. The sample sizes for the SIPP are 26,354 persons for the SIPP/SSA matched data (S0, S2)—4,727 of whom are Medicare beneficiaries and 30,271 persons for the SIPP survey data only (S1)—5,180 of whom are Medicare beneficiaries. The sample size for the HRS is 16,060 persons—10,725 of whom are Medicare beneficiaries. | ||||||
For the SIPP analysis, we show LIS eligibility estimates using survey data alone (S1) to contrast with those from the baseline (S0) using the matched survey/administrative data. (The (S2) result is based on another sensitivity analysis discussed at the end of this section.) Large discrepancies between these estimates would point to a sizable impact of measurement error (presumably in the survey data), whereas small discrepancies would suggest that measurement error is not an important problem. In addition to being informative about the potential measurement errors in the income components and other variables that are present in the administrative data, this analysis could be considered tentative evidence of the overall quality of the data and thus give more or less confidence in the survey variables that have no administrative counterparts and, by implication, more or less confidence in the eligibility estimates. For the HRS, we can compare eligibility estimates using administrative or survey data for the same year only for 2002. But a similar exercise can be conducted that is restricted to the Medicaid/Medicare Savings variable for 2006, by comparing the results obtained using only survey data (H1) with results obtained by imputing Medicaid/Medicare Savings beneficiary status as done in the baseline (H0).13
The use of administrative data has a relatively small effect on the estimates, but does suggest that measurement error is important to account for (Table 5). Alternatives S1 and H1 produce the estimates that would result if administrative data were not available to replace error-ridden income components and program participation, in the case of the SIPP, and to impute Medicaid/Medicare Savings program eligibility, in the case of the HRS.14 In both cases, the comparison with the baseline estimates show little change, representing about 1–2 percent in the estimated absolute number eligible for the LIS and an equally modest change in the LIS eligibility rate. The S1 estimate of the number eligible for the LIS is lower than the S0 estimate, and a slightly higher fraction are automatically eligible; the reverse holds for H1 versus H0. This suggests that the self-reported income variables in the SIPP overstate countable income, and the program participation variables in the SIPP overstate Medicaid or SSI participation. As noted earlier, the self-reports of Medicaid eligibility in the HRS overstate Medicaid eligibility in the 2002 data (for the original HRS cohort). Hence, we would expect that the estimated number of eligibles, particularly automatically eligible, would be higher when using only the survey data, without Medicaid imputation. We see a higher total number of eligibles, but for the automatically eligible, we see the opposite. This implies that there is differential under- and overreporting among subgroups.
Because the estimates in Table 5 pertain to the specific populations covered by the SIPP and HRS, respectively, they do not indicate how our estimate of the total LIS-eligible population would change if we used alternative methods. In Chart 5, we reproduce the baseline estimates shown in Chart 4 (dark gray bars) and add three additional estimates (light gray bars) based on using survey data only for the SIPP (S1, H0), only for the HRS (S0, H1), or for both sources (S1, H1). (The fourth additional estimate (last light gray bar) will be discussed at the end of this section.) In each case, the total estimate is based on averaging the SIPP and HRS estimates when the subpopulations overlap. As with Chart 4, we continue to show the estimated 95 percent confidence intervals accounting for sampling error. The three additional estimates based on the use of survey data in place of administrative data show a range of 11.8 million (S1, H0) to 12.3 million (S0, H1). This difference of about 0.5 million is roughly one-fourth the variation compared with changing the weight placed on the two data sources (as shown in the range between the second and third dark gray bars of about 2.3 million) and within the error bands of the baseline estimate when the SIPP and HRS are weighted equally (first dark gray bar).
Point estimates and confidence intervals for baseline estimate of potentially LIS-eligible population in 2006, with selected sensitivity analyses
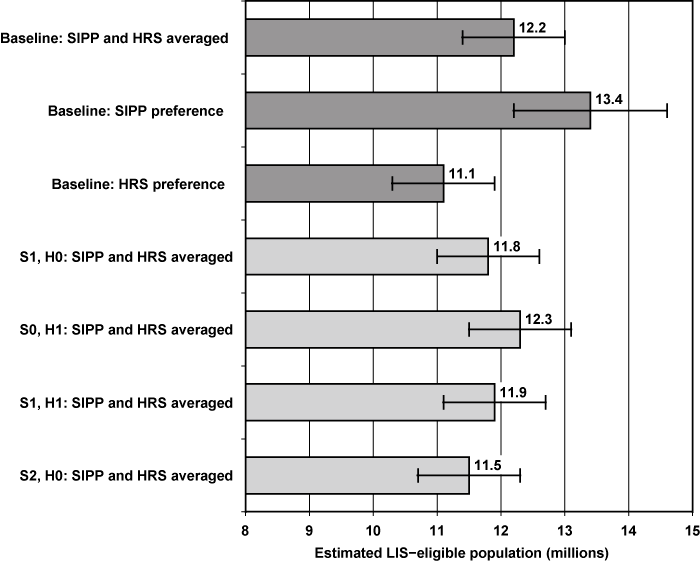
| Estimate | Estimated LIS-eligible population (millions) | Standard error | Bottom confidence interval | Top confidence interval |
|---|---|---|---|---|
| Baseline: SIPP and HRS averaged | 12.2 | 0.425 | 11.4 | 13.1 |
| Baseline: SIPP preference | 13.4 | 0.620 | 12.2 | 14.6 |
| Baseline: HRS preference | 11.1 | 0.406 | 10.3 | 11.9 |
| S1, H0: SIPP and HRS averaged | 11.8 | 0.394 | 11.0 | 12.6 |
| S0, H1: SIPP and HRS averaged | 12.3 | 0.424 | 11.5 | 13.2 |
| S1, H1: SIPP and HRS averaged | 11.9 | 0.393 | 11.1 | 12.6 |
| S2, H0: SIPP and HRS averaged | 11.5 | 0.402 | 10.7 | 12.3 |
Differential wealth distributions. Although the use of administrative data corrects for potential measurement error in income components and program participation, the bias appears to be relatively modest. Thus, the differences in the estimates for the SIPP and HRS cannot be explained by differential availability of matched administrative data. Another potential source of difference is in the quality of the wealth data for which there is no administrative data counterpart. In both surveys, we must rely on the self-reported survey data. Meijer, Karoly, and Michaud (2009) report striking differences in the distribution of countable resources in the SIPP versus the HRS.15 Notably, the 10th, 25th, and 50th percentiles are two to four times higher in the HRS than in the SIPP. Overall, the HRS resource distribution is shifted to the right of the SIPP distribution for both married and single Medicare beneficiaries such that the underlying distributional differences between the SIPP and HRS explain much of the differential estimates of LIS eligibility.
In the absence of administrative data with which to assess potential error in the measurement of countable resources, we must rely on other information about the quality of the survey data. The HRS has long been viewed as collecting high-quality data on wealth (and income) both because the survey instrument asks about a more disaggregated set of wealth components and because of the use of unfolding brackets to bound responses regarding each wealth component into specific ranges when a respondent is unwilling or unable to provide a specific figure (Juster and Smith 1997). Other recent innovations in the collection of income data in the HRS, along with the long-standing use of unfolding brackets, have been demonstrated to improve the quality of both the income and asset measures (Hurd, Juster, and Smith 2003). In contrast, the recent analysis of asset distributions in the SIPP by Scholz and Seshadri (2008) suggests that the SIPP underestimates assets, especially for individuals at the bottom of the income distribution. On the other hand, Sierminska, Michaud, and Rohwedder (2008) show that the HRS wealth distribution matches the SCF wealth distribution relatively well, particularly at the bottom of the distribution (below the 25th percentile). This suggests placing relatively more weight on the HRS estimates of LIS eligibility (that is, weighting toward the bottom bar in Chart 4) or, at most, weighting the two data sources equally as we do in our baseline estimate (top bar).
As an alternative to reweighting the contribution of the SIPP and HRS data to the estimate of LIS-eligibles, we perform an additional sensitivity analysis. In particular, alternative S2 in Table 5 is based on rescaling the SIPP wealth distribution for the entire SIPP population using a scaling factor that matches the median of the SIPP distribution to the median of the HRS distribution for the population where they overlap (that is, the noninstitutionalized population aged 53 or older). The resulting upward shift in the SIPP wealth distribution leads to a large reduction in the estimated LIS-eligible population shown in panel A—a decline of about 1.4 million (or 11 percent) over S0 and a 3.4 percentage-point reduction in the eligibility rate. The last light gray bar in Chart 5 shows the result when S2 and H0 are combined to generate an overall estimate of LIS-eligibles where, like the baseline, we continue to use equal weights for the SIPP and HRS where the populations overlap. The estimate of 11.5 million is close to the estimate of 11.1 million when the HRS is given preference (third dark gray bar), which would be justified if the HRS wealth distribution was closer to the true distribution compared with the SIPP.
Conclusions
The objective of this study was to generate an estimate of the LIS-eligible population as of January 2006, using the best available data. Our reliance on survey data from the SIPP and HRS, combined with matched administrative data from SSA, represents an advance over previous estimates in using administrative data where possible to substitute for potentially error-ridden survey measures of income and program participation. In addition, we have addressed several other methodological challenges including the need to cover the population of interest, to correct for potential bias from selective panel attrition and data matching, and to replicate the LIS eligibility rules as closely as possible. The use of sensitivity analyses allows us to consider the robustness of our results to the use of survey versus administrative data and to consider the sensitivity of our estimates to other methodological choices.
The baseline methodology we use to derive estimates for 2006 combines results from the SIPP and HRS with equal weights for the overlapping population (noninstitutionalized persons aged 53 or older) and otherwise uses estimates from either the SIPP or HRS for the other population subgroups. The baseline estimates use the matched SIPP/Social Security administrative data and impute Medicaid/Medicare Savings participation for the HRS. We also use attrition-adjusted and matching-adjusted (SIPP only) weights and rescale the weights to match known marginal distributions for the population. Based on this approach, we estimate that 12.2 million Medicare beneficiaries (or 29 percent) were potentially eligible for the LIS in 2006. Accounting for sampling error, the 95 percent confidence interval is from 11.4 million to 13.1 million. The error band would be wider if we also accounted for modeling uncertainty.
The sensitivity analysis shows that the baseline estimate is most sensitive to the weight placed on the estimates derived from the SIPP versus the HRS. Our baseline method gives those data sources equal weight. If we instead give preference to the SIPP-based estimates and use the HRS only when it is the sole source of data for a subpopulation, the estimated number of LIS-eligibles increases from the baseline of 12.2 million to 13.4 million. If we alternatively give preference to HRS-based estimates, the estimate falls to 11.1 million. Accounting for sampling error alone, the confidence intervals around these three estimates range from a lower bound (based on the HRS-preference result) of 10.3 million LIS-eligibles to an upper bound (based on the SIPP-preference result) of 14.6 million eligibles.
When the results are compared with and without the matched administrative data, we find modest differences in the estimate of the number of LIS-eligibles with the populations covered by the SIPP and the HRS—differences representing 1–2 percent. The estimates indicate that self-reported income and program participation variables in the SIPP overstate countable income and Medicaid or SSI participation. In the HRS, the self-reports of Medicaid eligibility overstate Medicaid eligibility in the 2002 data (for the original HRS cohort), but applying the resulting imputation model to the 2006 data shows that there is differential over- and underreporting among different subgroups. This suggests that measurement error in the survey measures of income and program participation is important to account for. Nevertheless, when the estimates from the two data sources are combined to generate an overall population estimate of LIS-eligibles, based on survey data alone in either or both of the data sources, the estimates range from 11.8 to 12.3 million—about one-fourth the variation compared with changing the weight placed on the two data sources using matched data.
Differences in the wealth distributions in the SIPP and HRS, for which there is no comparable administrative data, is another important source of variation in the estimates between the two data sources. If we adjust the SIPP wealth distribution based on a scaling factor consistent with the HRS distribution, the resulting estimate of LIS-eligibles is close to that obtained when the HRS is given preference. A number of other studies suggest that the HRS wealth distribution is more accurate, thereby lending support for giving greater weight to the HRS, either in how the estimates are combined or through adjusting the SIPP wealth distribution.
Given the issues with the quality and representativeness of the SIPP and HRS data identified in this article and the larger study on which it is based, future estimates of the LIS-eligible population would benefit from further analyses regarding the validity of the income, wealth, and program participation measures in the two data sources as well as the representativeness of the survey samples, especially for the low-income population. Such analyses can take advantage of the ability to match survey and administrative data using these two important sources of longitudinal data.
Notes
1 Other objectives of the larger study included examining the characteristics of the LIS-eligible population and projecting the size of the eligible population for 2008. See Meijer, Karoly, and Michaud (2009) for those results.
2 Administrative data also typically lack the full range of individual or family characteristics (for example, marital status, education level, health status) that might be of interest in examining the characteristics of the eligible and noneligible populations.
3 Only individuals who were in the target age groups but already in nursing homes at the time of sampling are missed. The numbers of such individuals are negligible for the HRS, War Baby (WB), and Early Baby Boomer (EBB) cohorts. For the Assets and Health Dynamics Among the Oldest Old (AHEAD) and Children of the Depression Age (CODA) cohorts, however, this is a nonnegligible bias at the time of sampling. But the selectivity bias tends to disappear very quickly. For example, Adams and others (2003) found that mortality rates between waves 1 (1993) and 2 (1995) in the AHEAD were substantially below the life tables, but this difference had vanished almost completely between waves 2 and 3 (1998).
4 As discussed in the next section, we also use data from the January 2006 Current Population Survey (CPS) and the 2004 National Nursing Home Survey (NNHS) to reweight the SIPP and HRS data, after correcting the weights to account for selective attrition and matching, in order to match the known demographic distribution of the population.
5 The match rate for individual records is slightly higher, but for determining LIS eligibility, we need spousal information; therefore, the respondents who are successfully matched, but whose spouses are not, are not in our matched sample.
6 The model results are available in Meijer, Karoly, and Michaud (2009). See Davern, Klerman, and Ziegenfussi (2007) for a similar model for the CPS.
7 Using the SIPP, we can also compare survey measures with administrative measures at the individual level using 2006 data, or we can compare their marginal or joint distributions. Most relevant for our purposes is comparing the fraction of individuals whose countable incomes exceed the threshold for LIS eligibility, depending on whether survey or administrative income data are used. As discussed in Meijer, Karoly, and Michaud (2009), this comparison shows differences of less than 2 percentage points, which is fairly small and supports our decision not to incorporate measurement-error corrections in the HRS.
8 The LIS administrative data allow us to assess the reasonableness of this assumption. Meijer, Karoly, and Michaud (2009) show that upward of 70–80 percent of LIS applicants with resources near the eligibility threshold (that is, those below the threshold, measured as 80–100 percent of the threshold, and those above the threshold, measured as 100–120 percent of the threshold) claimed the exclusion of expenses for a funeral and/or burial. Thus, our assumption of 100 percent exclusion is not unreasonable and provides a lower bound on countable resources.
9 From the combined CMS/NNHS data, we estimate the size of this population to have been about 75,000 in 2006. Hence, the underestimation of the number of LIS-eligibles because of this omission is relatively small.
10 See Meijer, Karoly, and Michaud (2009) for additional detail. The standard errors do not take uncertainty about the eligibility variables into account—uncertainty that results, for example, from imputing Medicaid/Medicare Savings beneficiary status in the HRS.
11 See Meijer, Karoly, and Michaud (2009) for results separately by institutionalization status and by data source.
12 In addition to the sensitivity analysis reported here, Meijer, Karoly, and Michaud (2009) also consider the sensitivity of the estimates to other variations in the methodology such as assumptions about funeral/burial expenses, household composition, whether 401(k) balances are included in countable resources, and the method of reweighting the attrition- and match-adjusted weights to match CPS marginals.
13 The estimates shown in Table 5 for S1 and H1 correspond to those reported in Meijer, Karoly, and Michaud (2009) as S3 and H3. The alternative S2, discussed later in this section, corresponds to S6 in the full study.
14 Note that this means that the SIPP sample will include cases that do not have a match with administrative data and that both sources will use weights that adjust only for panel attrition and reweight to the CPS.
15 Differences in countable income are considerably smaller.
References
Adams, Peter, Michael D. Hurd, Daniel McFadden, Angela Merrill, and Tiago Ribeiro. 2003. Healthy, wealthy, and wise? Tests for direct causal paths between health and socioeconomic status. Journal of Econometrics 112(1): 3–56.
Bound, John, Charles Brown, and Nancy Mathiowetz. 2001. Measurement error in survey data. In Handbook of Econometrics, Volume 5, James J. Heckman and Edward Leamer, eds., 3705–3843. Amsterdam: Elsevier.
Brownstone, David, and Robert G. Valletta. 1996. Modeling earnings measurement error: A multiple imputation approach. Review of Economics and Statistics 78(4): 705–717.
Card, David, Andrew K. G. Hildreth, and Lara D. Shore-Sheppard. 2004. The measurement of Medicaid coverage in the SIPP: Evidence from a comparison of matched records. Journal of Business and Economic Statistics 22(4): 410–420.
[CMS] Centers for Medicare and Medicaid Services. 2006. LIS-eligible Medicare beneficiaries with drug coverage, as of 5-7-2006. Washington, DC: Department of Health and Human Services. Available at http://www.cms.gov/States/Downloads/LISBenesCount.pdf.
———. 2007. 2007 enrollment information. Washington, DC: Department of Health and Human Services. http://www.cms.gov/PrescriptionDrugCovGenIn/ (accessed December 15, 2008).
———. 2008. 2008 enrollment information. Washington, DC: Department of Health and Human Services. http://www.cms.gov/PrescriptionDrugCovGenIn/ (accessed December 15, 2008).
Congressional Budget Office. 2004. A detailed description of CBO's cost estimate for the Medicare prescription drug benefit. Washington, DC. Available at http://www.cbo.gov/doc.cfm?index=5668.
Czajka, John L., Jonathan E. Jacobson, and Scott Cody. 2003. Survey estimates of wealth: A comparative analysis and review of the Survey of Income and Program Participation. Final report. Washington, DC: Mathematica Policy Research.
Davern, Michael, Jacob Alex Klerman, and Jeanette Ziegenfussi. 2007. Medicaid under-reporting in the Current Population Survey and one approach for a partial correction. Working Paper No. WR-532. Santa Monica, CA: RAND Corporation. Available at http://www.rand.org/pubs/working_papers/WR532/.
General Accounting Office. 2004. Medicare Savings programs: Results of Social Security Administration's 2002 outreach to low-income beneficiaries. Report No. GAO-04-363. Washington, DC: General Accounting Office. Available at http://www.gao.gov/cgi-bin/getrpt?GAO-04-363.
Haider, Steven, and Gary Solon. 2000. Nonrandom selection in the HRS Social Security earnings sample. Unrestricted Draft No. DRU-2254-NIA. Santa Monica, CA: RAND Corporation. Available at http://www.rand.org/pubs/drafts/DRU2254/.
Hurd, Michael, F. Thomas Juster, and James P. Smith. 2003. Enhancing the quality of data on income: Recent innovations from the HRS. Journal of Human Resources 38(3): 758–772.
Juster, F. Thomas, and James P. Smith. 1997. Improving the quality of economic data: Lessons from the HRS and AHEAD. Journal of the American Statistical Association 92(440): 1268–1278.
Kapteyn, Arie, Pierre-Carl Michaud, James P. Smith, and Arthur Van Soest. 2006. Effects of attrition and non-response in the Health and Retirement Study. RAND Working Paper No. WR-407. Santa Monica, CA: RAND Corporation. Available at http://www.rand.org/pubs/working_papers/2006/RAND_WR407.pdf.
Little, Roderick J., and Donald B. Rubin. 2002. Statistical analysis with missing data, 2nd edition, New York, NY: John Wiley & Sons, Inc.
McClellan, Mark B. (administrator). 2006. Centers for Medicare and Medicaid Services, testimony before the House Committee on Ways and Means, hearing on Medicare prescription drug benefit, June 14. Available at http://www.cms.gov
Meijer, Erik, Lynn A. Karoly, and Pierre-Carl Michaud. 2009. Estimates of potential eligibility for low income subsidies under Medicare Part D, Technical Report No. TR-686. Santa Monica, CA: RAND Corporation. Available at http://www.rand.org/pubs/technical_reports/TR686/.
National Institute on Aging. 2007. Growing older in America: The Health and Retirement Study. Bethesda, MD: National Institute on Aging. Available at http://www.nia.nih.gov/ResearchInformation/ExtramuralPrograms/BehavioralAndSocialResearch/HRS.htm.
Olson, Janice A. 1999. Linkages with data from Social Security administrative records in the Health and Retirement Study. Social Security Bulletin 62(2): 73–85. Available at http://www.socialsecurity.gov/policy/docs/ssb/v62n2/v62n2p73.pdf.
Rice, Thomas, and Katherine A. Desmond. 2005. Low-income subsidies for the Medicare prescription drug benefit: The impact of the asset test. Menlo Park, CA: The Henry J. Kaiser Family Foundation (April).
———. 2006. Who will be denied Medicare prescription drug subsidies because of the asset test? American Journal of Managed Care 12(1): 46–54.
Scholz, John Karl, and Ananth Seshadri. 2008. The assets and liabilities held by low-income families. Research Paper. Madison, WI: University of Wisconsin (September 9). Available at http://www.ssc.wisc.edu/~scholz/Research/Assets_Poverty.pdf.
Sierminska Eva, Pierre-Carl Michaud, and Susann Rohwedder. 2008. Measuring wealth holdings of older households in the U.S.: A comparison using the HRS, PSID and SCF. Paper presented at the Pensions, Private Accounts, and Retirement Savings Over the Life Course workshop, Ann Arbor, MI (November 20–21). Available at http://psidonline.isr.umich.edu/Publications/Workshops/2008/LC/MRS_WealthCompsv10.pdf.
St. Clair, Patricia, Darlene Blake, Delia Bugliari, Sandy Chien, Orla Hayden, Michael Hurd, Serhii Ilchuk, and others. 2008. RAND HRS data documentation, version H. Santa Monica, CA: RAND Corporation, Center for the Study of Aging.
Wansbeek, Tom, and Erik Meijer. 2000. Measurement error and latent variables in econometrics. Amsterdam: Elsevier.
Westat. 2001. Survey of Income and Program Participation User Guide, 3rd edition. Washington, DC: Census Bureau.